Section 7 - Sparse Matrices

2B.7.1 Memory Overload

Imagine this simple problem: You are asked to represent the connections between 1000 components on an electronic circuit board in a program. Perhaps there are conductive wires between some of the components, and we are storing the distance of each electronic pathway to find out how fast a signal can travel, at the speed of light, from one component to the next. The project lead wants us to store this data in matrix form: a 1000 x 1000 matrix where the values in position (r, c) is the distance or value between component #r and component #c. This matrix has 1,000,000 entries. However, each component may only be connected to a few others, making the vast majority of these 1,000,000 values 0. So allocating a 1000 x 1000 matrix would be wasteful. The matrix is considered sparse, because most the values are 0.

In physics research, particle interactions are similarly connected with each other at the quantum level, but given the vast number of particles, the connections themselves only represent a tiny fraction of the possible elements in a matrix whose rows and columns are the particles and whose entries are some data about the interaction of those particles.

A database of individuals around the world might consist of marketing, security or health information about pairs or small groups of individuals (store the relationship between Kevin Bacon and Albert Einstein), but we still need every individual represented. Again, a matrix whose rows and columns represent the individuals and whose entries are the relationships between each two individuals is sparse.

Sometimes sparse matrices are represented by images whose edges are the connections between the data in the set. This is a graphic of one such representation taken at University of Florida (the matrix is 10,302 x 10,302, but there are really only 20,199 entries, compared with the 10 million needed if the matrix were stored in standard array format. Here are other images from that archive:

2B.7.2 A Sparse Matrix Representation

There are many ways one can store and manipulate sparse matrix data, and one of them uses graphs, an ADT which is the pinnacle of our course and the topic of weeks ten and eleven. However there is a very nice approach we can implement here and now that uses vectors and lists, combined.

Imagine that we have an M x M matrix where M is, say 100,000. That would be a huge matrix to attempt to create in main memory in a program on your home or even work computer. (Try it - you can't, not even dynamically!) It may be that there are very few entries in the matrix that are different from 0. I'll say, for illustration, that there are only three non-zero elements, stored at locations (2, 995), (981, 570) and (981, 1617). We can create a vector of pointers of size M ( equal to 100,000, say), and each pointer represents row. If there is something in that row, then the pointer points to a list of one or more non-zero entries. Here is the picture:

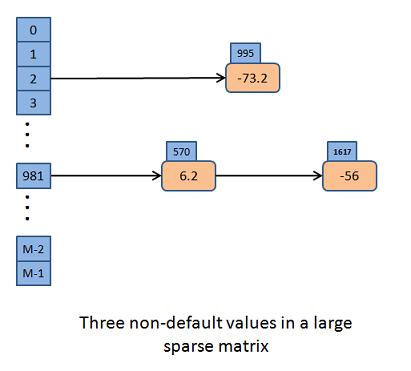
Notice that the three nodes stored in this data structure contain both the data (say -73.2) as well as the column number (995). In normal matrices, we don't store the column number because it is implied by the index (array[2][995]). But with sparse matrices, we are saving so much space by not having the normal [row][col] implied storage paradigm, we need a way to know what row and column the data is in. We must store the column in the node.

We don't need to store the other values since they are all 0. If someone wants to read a value from this matrix, we ask them the row and column value. We go down the master vector on the left to get the row, and then move across that row's list looking for a node whose column value matches the desired column. It should only take a couple node "hops" to get to the end of the list since most rows are blank, and those that aren't have one or two nodes, at most. If we find a node with the desired column, we read the data value from it. If not, we tell the client that the value is 0, because, after all, that's what it means when no node is in the sparse matrix.

If the client wants to write something in the table, we see if that row and column node is already occupied. If so, we just change the data. If not, we add a node to the list and put the column number and data value into it. Oh, and what if they want to store the default value? In that case we may have to do nothing (but not necessarily!)

2B.7.3 Implementation

We'll need some node type (see your assignment for a complete solution to that, provided by your instructor). Then, the sparse matrix class would have one vector (the master column on the left) and each item in the vector will be a list for the corresponding row. So, in reality, rather than it being a vector of pointers, it is a vector of lists. In a newly constructed sparse matrix, all the lists are blank. The only thing we need from the client is:

The size of the matrix so we know how large to make the vector (and a way to do range checking), and
The default value, usually 0. This way, we know not to store the 0 if the user tries to set an element to that value - no need: we assume everything not stored is 0. Also, we know what value to return to the user if we don't find a node in the sparse matrix.

The client works with this as if it were a normal matrix, with a little different syntax. Here's an example:

   SparseMat<int> mat(10000, 10000, 0);
    
   mat.set(4,4) = 55;
   cout << mat.get(7, 8) << endl;

Of course, we get range checking and all the other goodies, by using this, rather than a real array.

The protected (rather than private) data and data types in our SparseMat class template goes something like this:

// use protected, not private, in anticipation of a future subclass
protected:
   typedef FHlist< MatNode<Object> > MatRow;
   typedef FHvector<MatRow> MasterCol;
   
   MasterCol rows;
   Object defaultVal;
   int rowSize, colSize;

The rest is pretty much just careful counting and logic. This is a very fun second "warm-up" project for the quarter which you will get to do this week. I have outlined what you need to do in the narrative above, so you'll have to read it a few times as you work.

Next week, we will break new ground by getting theoretical (and theatrical) - you'll sound like a bunch of genius of Ph.D.s after that.

Until then, do a careful job on this sparse matrix implementation using our FHlist and FHvector (yes, these are required because I need you to exercise their use for the treacherous AVL trees and quadratic probing hash tables that will come during out action-packed and dramatic mid-quarter).

2B.7.4 A C++ Notational Detail

In the implementation of two or three of your methods, you'll have occasion to use an iterator, and you will declare it something like this:

   MatRow::iterator iter;

This seems correct, but technically, it isn't. It will actually work in Visual C++, but not in all compilers. The reason is too technical for me to get into in a way that will be palatable at this point, so I will simply "give" you the repair and you can use it without further explanation. The line requires a C++ keyword "typename" in front of it:

   typename MatRow::iterator iter;

If you get a compiler error when trying to declare any iterator in these classes, chances are that adding "typename" in the front of the declaration will fix it. To be continued.