Section 6 - Indirect Sort Completed

9A.6.1 The Need For An In-Place Completion to Indirect Sort

The final stage of the indirect sort was already outlined and in fact can be implemented by copying the coding ideas that were presented earlier. If we do that, we would instantiate a second large object array, a2[] and use two loops to untangle and then replace the sorted values back into the client array.

There are two problems with this approach.

1. It takes too much memory.
2. It takes too long.

I don't mean that it can't be used in some situations, but if you start experimenting with the kinds of large objects and the sizes of the arrays that result in sluggish simple sorts, you end up very close to the memory capacity of the machine. For example, right about the time you discover that you have a large array -- of say, 10,000 objects -- which is taking too long to sort, and you try to expand that to 100,000 elements, you might find this:

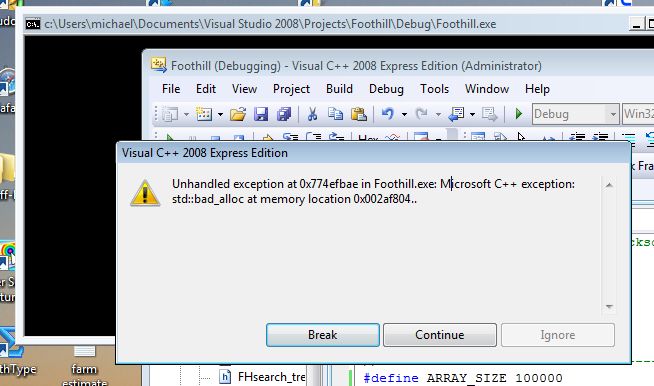
We just broke the runtime space of a system with 6 (usable) Gig of RAM. Why? Because in this case, we had large objects (3000 floats in each) and a large array (100,000). 3000 floats is 12,000 bytes. This makes the array really big - 1.3 billion, all by itself. Try duplicating that just so you can untangle the indirectly sorted array and you end up crossing the OS blood-brain boundary.

Thus, it behooves us to do an in-place untangling operation. That is what the third and final part of the indirect sort does.

9A.6.2 Untangling the Sorted Array

The logic behind this algorithms is just at the limit of what I can easily explain with pictures and words. Therefore, I'm going to skip the pep talk and ask you to either read it in the book or work on it with pencil and paper. While it is not terribly difficult, the exact technique is not going to be used for much other than indirect array untangling.

   // untangle the client elements so they match the pointer order
   for(k = 0; k < a.size( ); k++ )
      if( p[k] != &a[k] )
      {
         tmp = a[k];
         for(j = k; p[j] != &a[k]; j = nextJ)
         {
            nextJ = p[j] - &a[0];
            a[j] = *p[j];
            p[j] = &a[j];
         }
         a[j] = tmp;
         p[j] = &a[j];
      }

I will talk about two lines that do the simple work, though. First this line:

      a[j] = *p[j];

Here we are doing, exactly, what the untangling process entails. The idea is that in the pointer array, position j represents the jth largest element. That is, p[j] points to the jth largest elements. What we want to do, however, is get the jth largest element into the jth position of the client array, a[j]. And this is exactly what that statement does. By observing the overloading of the * operator on p[j], we are copying the value of the object pointed to by p[j] into its true final position in the client array a[j].

      p[j] = &a[j];

In this line, we ask the p[j] pointer to follow the data that it just copied into its new location. In other words, after the last assignment, the jth largest value is in its new home, a[j], and we want p[j] to continue to point to it. This step is needed for the algorithm to work. When we are finished, of course, we don't need p[] so what it points to is not relevant. However, during the process of untangling, we have to avoid destroying important data and pointers.

The rest of the code requires realizing that the two arrays, p[] and a[] can be partitioned into a a set of mutually exclusive "cycles". The inner loop untangles each cycle, completely, and once that is done, the outer loop looks for the next cycle to untangle.

If I go too much further, I will break my word and start trying to explain too much, resulting in confusion, so I'll stop here.

9A.6.3 The Full Indirect Sort

Here, then, is the full function, minus the SmartPointer class which you can get from the last page (or the FHsort.h include fine):

// indirect sort - uses SmartPointer as intermediate type
template <typename Comparable>
void indirectSort( FHvector<Comparable> & a )
{
   int k, j, nextJ, arraySize = a.size();
   Comparable tmp;
   FHvector< SmartPointer<Comparable> > p(arraySize);

   // point each smart pointer to its corresponding client object
   for( k = 0; k < arraySize; k++ )
      p[k] = &a[k];

   // do the sort - it only changes the smart pointer order
   quickSort(p);

   // untangle the client elements so they match the pointer order
   for(k = 0; k < a.size( ); k++ )
      if( p[k] != &a[k] )
      {
         tmp = a[k];
         for(j = k; p[j] != &a[k]; j = nextJ)
         {
            nextJ = p[j] - &a[0];
            a[j] = *p[j];
            p[j] = &a[j];
         }
         a[j] = tmp;
         p[j] = &a[j];
      }
}

We have already done some benchmarking on this, which means we are done.