Section 4 - Indirect Sort

9A.4.1 Large Objects

We now consider the effects of "sluggish" underlying data types. This includes any class whose copy operation takes significantly longer than a primitive int copy. One way this might occur is if the class has a large data footprint causing a lot of bytes to be transferred when an object assignment is encountered. Another possibility is that the class has complicated deep memory whose copy, or cloning, operation requires allocation and processing. In these situations, the simple act of a[k] = a[k-1], which appears in the kernel of any sort loop, will be stressful enough to degrade performance.

To illustrate the point, consider a hypothetical class which consists of several members, one of which is an array of floats. One application where this might occur is in a particle accelerator detector, where each collision of particles generates lots of data (for that one "event", and we have tons of events. Here is a stripped-down version of such a class:

class HadronCollisionEvent
{
private:
   static const int NUM_FLOATS = 50; // or anything from 1 to 100000 say

   string name;
   int sortKey;
   float fltVals[NUM_FLOATS];
   
public:
   int getKey() { return sortKey; }
   void setKey(int n) { sortKey = n; }

   bool operator<(const HadronCollisionEvent &rhs)
   {
      return (sortKey < rhs.sortKey);
   }
};

The class contains an array whose size, NUM_FLOATS, is controlled by a class constant. For your reference, here is the client we will be using to analyze the situation:

// Comparison of mergeSort and quickSort on large objects
#include <iostream>
using namespace std;
#include "FHsort.h"
#include "FHvector.h"
#include <time.h>

#define ARRAY_SIZE 10000

class HadronCollisionEvent
{
private:
   static const int NUM_FLOATS = 50;  // modify from 1 to 3000 for testing

   string name;
   int sortKey;
   float fltVals[NUM_FLOATS];
   
public:
   int getKey() { return sortKey; }
   void setKey(int n) { sortKey = n; }

   bool operator<(const HadronCollisionEvent &rhs)
   {
      return (sortKey < rhs.sortKey);
   }
};

// --------------- main ---------------
int main()
{
   int k;
   HadronCollisionEvent *arrayOfObjs;
   FHvector<HadronCollisionEvent> fhVectorOfObjs;
   FHvector<HadronCollisionEvent> fhVectorOfObjs2;
   clock_t startTime, stopTime;

   arrayOfObjs = new HadronCollisionEvent[ARRAY_SIZE];

   // build both an array and a vector for comparing sorts
   for (k = 0; k < ARRAY_SIZE; k++)
   {
      arrayOfObjs[k].setKey( rand()%ARRAY_SIZE );
      fhVectorOfObjs.push_back(arrayOfObjs[k]);
      fhVectorOfObjs2.push_back(arrayOfObjs[k]);
   }

   startTime = clock();  // ------------------ start 
   quickSort(fhVectorOfObjs);
   stopTime = clock();  // ---------------------- stop
   cout << "\nquickSort Elapsed Time: " 
      << (double)(stopTime - startTime)/(double)CLOCKS_PER_SEC 
      << " seconds." << endl << endl;

   startTime = clock();  // ------------------ start 
   mergeSort(fhVectorOfObjs2);
   stopTime = clock();  // ---------------------- stop
   cout << "\nmerge sort Elapsed Time: " 
      << (double)(stopTime - startTime)/(double)CLOCKS_PER_SEC 
      << " seconds." << endl << endl;

   for (k = 0; k < ARRAY_SIZE; k+= ARRAY_SIZE/5)
   {
      cout << "quickSort #" << k << ": " 
         << fhVectorOfObjs[k].getKey() << ", ";
      cout << "merge sort #" << k << ": " 
         << fhVectorOfObjs2[k].getKey() << endl;
   }

   delete[] arrayOfObjs;
   return 0; 
}

To start, we see how the constant (internal float array size, NUM_FLOATS) affects running time. We will sort using both mergeSort and quickSort. If each of the 10,000 objects has 10 floats here is the output:

quickSort Elapsed Time: 0.016 seconds.


merge sort Elapsed Time: 0 seconds.

[snip]
Press any key to continue . . .

But when we change NUM_FLOATS to 1000, and do not touch the size of the vector that we are sorting (still, 10,000), we get this result:

quickSort Elapsed Time: 0.14 seconds.


merge sort Elapsed Time: 0.468 seconds.

[snip]
Press any key to continue . . .

Clearly, the heavier objects have more inertia. Our goal next is to describe a sorting technique called indirect sort which will help alleviate this problem.

9A.4.2 Pointers As Proxies

The idea behind indirect sort is to use lightweight proxy objects in place of the original objects for the sort. The lightweight object of choice is an int or a pointer. We use pointers. Start out by creating a parallel array with the original, whose elements are pointers to the original objects. Here is the picture:

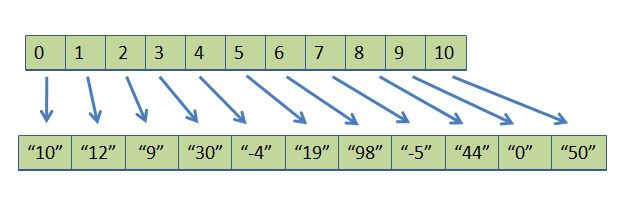
I have put double quotes, " ", around the values in the client array to indicate that these are not ints, but large objects whose keys are the value indicated. "12" is less than "30" because 12 and 30 are the two keys, respectively, but there is a lot more data in each object, to be sure. Also, the pointer array seems to contain ints, but really, 0 simply means "a pointer which points to the 0th client element", and 4 simply means "a pointer which points to the 4th client element". We will call the original, bottom, array the client array, a[], and the upper, manufactured, array the pointer array, p[].

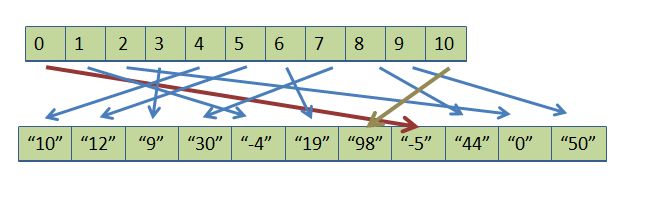
Next, we will perform a sort -- any sort (but why not quick, since it's the fastest?) with the following twist. We compare objects using the values in the client array, but when it comes time to swap elements, we only swap elements in the pointer array. Thus, the client array does not change, so no heavy lifting takes place. After the sort is complete the pointers have been rearranged so that p[0] points to the smallest client object, p[1] to the next smallest, and so on until p[10] (in our example) points to the largest. Here is the tangled mess, with the first and last pointers highlighted so you can easily see that they do, indeed, point to the smallest and largest client objects:

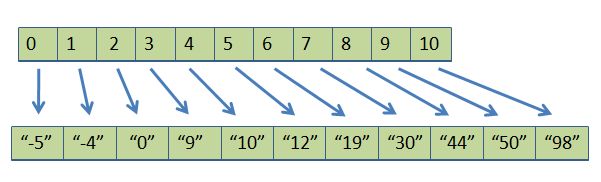
Finally, we have to untangle the mess by moving by really moving client objects so that the smallest ends up in a[0] and the largest ends up in a[10]. One way to think about this is by creating a second temporary object array, a2[], and using the pointers to fill this array, as in:

   for (k = 0; k < arraySize; k++)
      a2[k] = *(p[k]);

The result is the ordered array (in a2[]). But we have to copy the results back into a[], since that's what our client passed us, so we would need one more loop:

   for (k = 0; k < arraySize; k++)
      a[k] = a2[k];

What I just described has all the key ideas of indirect sort,but we have to handle some optimization and implementation details (don't we always?). Even with those details, the algorithm is no more complicated than it sounds. And it works. To prove it, I'll show you how indirect sort compares with quickSort on the 10,000 large HadronCollisonEvent objects.

quickSort Elapsed Time: 1.108 seconds.


indirect sort Elapsed Time: 0.171 seconds.

quickSort #0: 0, indirect sort #0: 0
quickSort #2000: 1590, indirect sort #2000: 1590
quickSort #4000: 3400, indirect sort #4000: 3400
quickSort #6000: 5610, indirect sort #6000: 5610
quickSort #8000: 7787, indirect sort #8000: 7787
Press any key to continue . . .

Ten times faster.

The implementation of indirect sort is tailored for C++ because of the magic of operator overloading. That's our next job, and it should be very revealing.