Section 3 - quickSort Observations

9A.3.1 Duplicate Paradox

There seems to be a slight inefficiency in quickSort. Continuing with the last graphic example let's go to the next pass of the outer loop, moving i right and j left until they each hit their next stopping point:

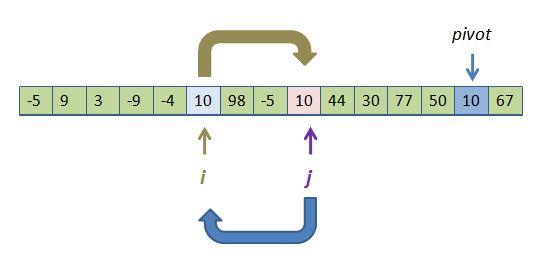
The inner loops indicate that we stop when a[i] = pivot (and same with a[j]). In this case we ended with both pointing to pivot. And as much as we can't stand the idea, we are about to swap two identical values. That hurts.

Did I lie when I said we were using a time-tested quickSort function? Surprisingly not. As with all other minutia regarding this coding, this has been painstakingly studied, and it has been found that attempts to avoid this unnecessary swap lead to worse situations. Here's an example. One thought would be to let i always move forward (right) when it hits an element == pivot:

   while( a[++i] <= pivot )
      ;
   while( pivot < a[--j])
      ;

What would it imply? In the current case, nothing too horrible. We would move i up one position, stop at 98 and then swap, 98 for 10:

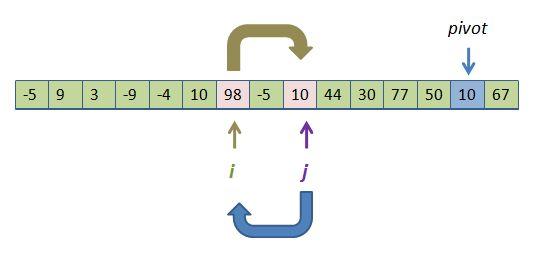
This results in the 10s "clumping" together (compared with before when they were actually staying on their own side of the tracks):

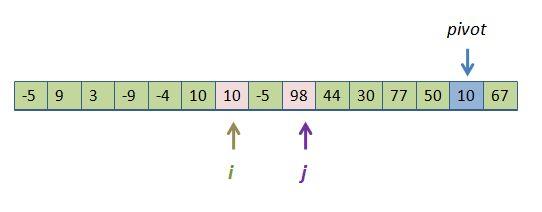
This seems innocuous. Imagine, though, that you have 1 million objects and 2% are the same, say 10. The plan just described would put them all on the left, causing that sub-array to have a bunch of 10s -- 20,000 of them -- clumped together in the left-sub array and passed to recursive quickSort call. (This scenario doesn't sound likely, but remember, we are only sorting on one field. If we were sorting on star "types", say, while there are billions of stars, there are only about 20 different types. These would very quickly form gigantic clumps of contiguous "equal" objects.) So, the strategy of letting i pass over pivots while j stops at them causes an immediate clumping of pivot values for the next generation of recursion. It leads, at lower levels of recursion to arrays that look like this:

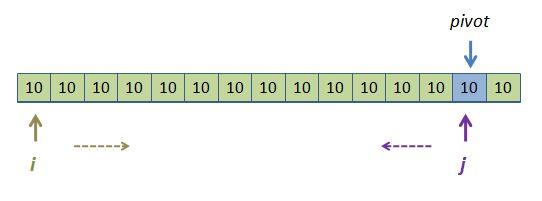
If you are really following along, you are thinking, "So what? Eventually these 10s need to end up next to each other anyway. The sooner we get them shoulder-to-shoulder the better." Let's see if that's true. Say we just entered this particular level of recursion and we have all these 10s in a large array as pictured above. Imagine that there are 1 million of them (again, possible if the sort key is something that a lot of items have in common). When we are all done with this level, i will slide all the way to the right and j will only move once due to the first pass of the j while loop. Here is what we get after this level of recursion runs its i and j loops:

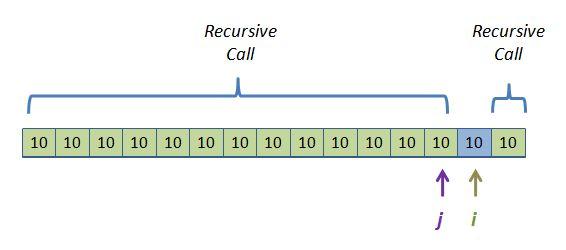
So our next recursive call will pass the left array, only two element smaller than we came in with, into a recursive quickSort call! This level of recursion resulted in extremely lopsided groups - something we know kills NlogN performance. Every subsequent recursive call from this level down will peel off two items in the left subgroup: the pivot and the right subgroup which consists of one item. With a million 10s in this recursion level, all the future left subgroups would have sizes 1million -2, 1 million - 4, 1 million - 6, etc. That's 500,000 recursive calls, rather than the expected log(1 million) = 20 calls we would have gotten if we had divided the groups up equally each time.

Summary

By trying to not swap equal values, we degraded the number of recursive calls to order N rather than order logN. This will cause very poor performance.