Section 2 - Coding quickSort
9A.2.1 Median Of Three Code
Our function, median3() will take the array, left and right as arguments and return a pivot. It gets the pivot by taking the median of the three values, but it has a happy side-effect: It sorts the three elements first, so that left ends up with the smallest of the three values in it and right has the largest. This guarantees that these two elements are in their proper sub-groups, so we don't really have to test them in the recursive quickSort function.
Here is the graphic:
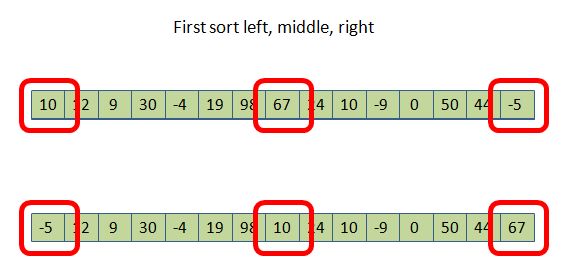
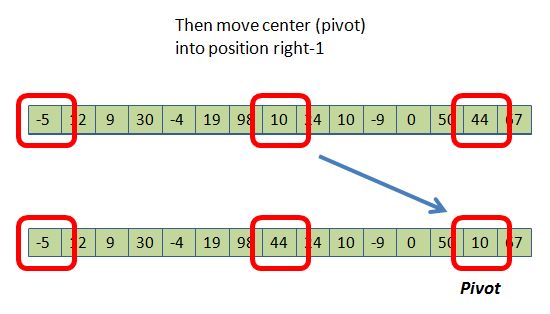
Look closely and you can see that not only are we moving the largest (67) into position right, but we also move the pivot into position right-1. This gets it "out of the way" so we can begin our quickSort partition step by operating on the array from positions 1 through right-2. We don't need to really test position 0 (which already contains a number < pivot, the -5), or right (which has a number > pivot, the 67), or even right-1 (which has pivot, 10, itself). (Don't worry about the 44 - it just happens to be what used to be in position right-1, and we had to swap it into the old middle position to allow the 10 to take its place at position right-1.)
When we are done partitioning this array into two sub-arrays, we will cleverly move the pivot back into the general population so that it is exactly between the two sub-groups and in its final position. But that is yet to come. For now, we look at the median3() code:
// median3 sorts a[left], a[center] and a[right].
// it leaves the smallest in a[left], the largest in a[right]
// and median (the pivot) is moved "out-of-the-way" in a[right-1].
// (a[center] has what used to be in a[right-1])
template <typename Comparable>
const Comparable & median3(FHvector<Comparable> & a, int left, int right)
{
int center;
center = (left + right) / 2;
if(a[center] < a[left])
mySwapFH(a[left], a[center]);
if(a[right] < a[left])
mySwapFH( a[left], a[right] );
if(a[right] < a[center])
mySwapFH(a[center], a[right]);
mySwapFH(a[center], a[right - 1]);
return a[right - 1];
}
Note that I use a self-made mySwapFH() function which is defined as you would expect (see FHsort.h). This is just a matter of doing it all oneself rather than calling the C++ swap() function.
9A.2.2 The Partition and Recursive Steps
At the highest level, we provide a public driver for the client. It calls the inner workhorse function like so:
template <typename Comparable>
void quickSort( FHvector<Comparable> & a )
{
quickSort(a, 0, a.size() - 1);
}
Next, we look at this so called "workhorse":
#define QS_RECURSION_LIMIT 15
template <typename Comparable>
void quickSort(FHvector<Comparable> & a, int left, int right)
{
Comparable pivot;
int i, j;
if( left + QS_RECURSION_LIMIT <= right )
{
pivot = median3(a, left, right);
for(i = left, j = right - 1; ; )
{
while( a[++i] < pivot )
;
while( pivot < a[--j])
;
if(i < j)
mySwapFH(a[i], a[j]);
else
break;
}
mySwapFH(a[i], a[right - 1]); // restore pivot
// recursive calls on smaller sub-groups
quickSort(a, left, i - 1);
quickSort(a, i + 1, right);
}
else
// non-recursive escape valve - insertionSort
insertionSort(a, left, right);
}
The first thing we notice as we read down the code is the recursive/escape test. If the array is smaller than QS_RECURSION_LIMIT we stop the recursion and call insertionSort(). This limit is set at 15 as discussed.
If the size of the incoming sub-array warrants continuing recursion, and therefore quickSort, we get a pivot from median3(). Next, we initialize two pointers, traditionally called i and j. These two pointers will help us move the smaller elements to the left side of the array, and the larger ones to the right.
The next phase is a loop. For each pass of the loop we will do the following:
- Move i right, skipping past elements that are correctly in the smaller sub-group and do not need to be moved.
- Move j left, skipping past elements that are correctly in the larger sub-group and do not need to be moved.
- When both i and j cannot skip any further elements, they are pointing to elements that are incorrectly positioned relative to pivot. When that happens, we swap them and repeat the loop.
Here is a picture. We start i and j at the two extremes:
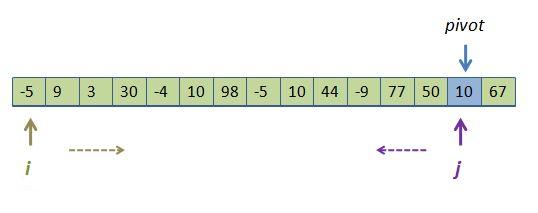
The two inner loops:
while( a[++i] < pivot )
;
while( pivot < a[--j])
;
cause i to go right, and j to go left, skipping over elements that are already in the correct sub-group. They each stop when they find an element in the wrong group. Here is where they would each first stop in the above array:
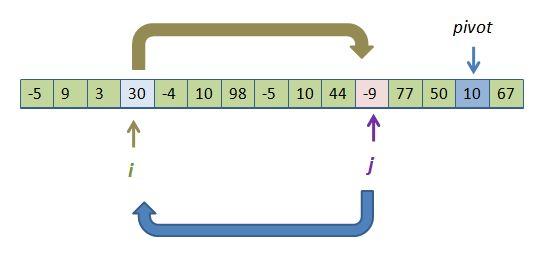
We mySwapFH() the two values, which fixes both problems at once, and continue our loop.
This loop continues until i crosses j, indicating we have completed the repositioning (or confirmation) of each item in the array.
At that stage, we can put pivot into location i (it just crossed paths with j and happens to point to the first element in the larger sub-group) using another mySwapFH().
Technical Note
I explained that the values in position left and right are already correct and position right-1 contains pivot which does not need to be "inspected". Therefore, we could start i at position left+1, j at position right-2, and move i right and j left from those starting locations. But if you look at the code, you'll see I start i one place back, at position left (not left+1) and j one place forward, at position right-1 (not right-2). Why?
Answer: Reading the code, further, you'll notice that we do ++i before we actually use it, so we are, in fact, beginning our examinations at position left+1. Similarly, we --j before we use it, so we are actually examining right-2 to start off, just as we should. That doesn't completely answer the question. It seems like we should not be so "cute". Start i and j where they really do start and increment them after we are done with each loop pass. This logic causes trouble (explained in the text). Without discussing that detail, I merely comment on it here.
9A.2.3 insertionSort
Our particular flavor of insertionSort does not admit an invocation that takes an array and a range. We have a version that takes an entire array (and operates on the whole thing). We need one that takes an array and a range. So we have to write yet another insertionSort(). It is easily done from the earlier version:
// version that takes vector and range
template <typename Comparable>
void insertionSort(FHvector<Comparable> & a, int left, int right)
{
int k, pos;
Comparable tmp;
for(pos = left + 1; pos <= right; pos++ )
{
tmp = a[pos];
for(k = pos; k > left && tmp < a[k - 1]; k--)
a[k] = a[k - 1];
a[k] = tmp;
}
}
9A.2.4 Benchmarks
I bet you're all curious to know the performance. Let's see that, even before the test client. Our fastest time so far has been the in-place heapSort() and we will compare against that (250,000 ints).
heap sort Elapsed Time: 0.021 seconds. quickSort Elapsed Time: 0.019 seconds. heap sort #0: 0, quickSort #0: 0 heap sort #50000: 6588, quickSort #50000: 6588 heap sort #100000: 13150, quickSort #100000: 13150 heap sort #150000: 19688, quickSort #150000: 19688 heap sort #200000: 26210, quickSort #200000: 26210 Press any key to continue . . .
On 250,000 ints seems 10% faster than heap. Increasing the array size causes the improvement to only get better, but we'd have to use dynamic arrays due to Windows compiler constraints. You can measure it on a Mac, though. Here's the client.
// Comparison of heapsort and quickSort vectors
#include <iostream>
using namespace std;
#include "Foothill_Sort.h"
#include "FHsort.h"
#include "FHvector.h"
#include <time.h>
// --------------- main ---------------
#define ARRAY_SIZE 250000
int main()
{
int k;
int arrayOfInts[ARRAY_SIZE];
FHvector<int> fhVectorOfInts;
FHvector<int> fhVectorOfInts2;
clock_t startTime, stopTime;
// build both an array and a vector for comparing sorts
for (k = 0; k < ARRAY_SIZE; k++)
{
arrayOfInts[k] = rand()%ARRAY_SIZE;
fhVectorOfInts.push_back(arrayOfInts[k]);
fhVectorOfInts2.push_back(arrayOfInts[k]);
}
startTime = clock(); // ------------------ start
heapSort(fhVectorOfInts);
stopTime = clock(); // ---------------------- stop
cout << "\nheap sort Elapsed Time: "
<< (double)(stopTime - startTime)/(double)CLOCKS_PER_SEC
<< " seconds." << endl << endl;
startTime = clock(); // ------------------ start
quickSort(fhVectorOfInts2);
stopTime = clock(); // ---------------------- stop
cout << "\nquickSort Elapsed Time: "
<< (double)(stopTime - startTime)/(double)CLOCKS_PER_SEC
<< " seconds." << endl << endl;
for (k = 0; k < ARRAY_SIZE; k+= ARRAY_SIZE/5)
{
cout << "heap sort #" << k << ": " << fhVectorOfInts[k] << ", ";
cout << "quickSort #" << k << ": " << fhVectorOfInts2[k] << endl;
}
return 0;
}
FH quickSort vs. STL sort
Here is the client:
// Comparison of heapsort and quickSort vectors
#include <iostream>
using namespace std;
#include "Foothill_Sort.h"
#include "FHsort.h"
#include "FHvector.h"
#include <algorithm>
#include <vector>
#include <time.h>
// --------------- main ---------------
#define ARRAY_SIZE 250000
int main()
{
int k;
int arrayOfInts[ARRAY_SIZE];
FHvector<int> fhVectorOfInts;
vector<int> stlVectorOfInts;
clock_t startTime, stopTime;
// build both an array and a vector for comparing sorts
for (k = 0; k < ARRAY_SIZE; k++)
{
arrayOfInts[k] = rand()%ARRAY_SIZE;
fhVectorOfInts.push_back(arrayOfInts[k]);
stlVectorOfInts.push_back( fhVectorOfInts[k] );
}
startTime = clock(); // ------------------ start
quickSort(fhVectorOfInts);
stopTime = clock(); // ---------------------- stop
cout << "\nquickSort Elapsed Time: "
<< (double)(stopTime - startTime)/(double)CLOCKS_PER_SEC
<< " seconds." << endl << endl;
startTime = clock(); // ------------------ start
// a pure stl sort - STL's best effort on its own vector types
sort(stlVectorOfInts.begin(), stlVectorOfInts.end());
stopTime = clock(); // ---------------------- stop
cout << "\nSTL Elapsed Time: "
<< (double)(stopTime - startTime)/(double)CLOCKS_PER_SEC
<< " seconds." << endl << endl;
for (k = 0; k < ARRAY_SIZE; k+= ARRAY_SIZE/5)
{
cout << "quickSort #" << k << ": " << fhVectorOfInts[k] << ", ";
cout << "STL sort #" << k << ": " << stlVectorOfInts[k] << endl;
}
return 0;
}And the results with optimization on:
// 250000 ints quickSort Elapsed Time: 0.018 seconds. STL Elapsed Time: 0.018 seconds. quickSort #0: 0, STL sort #0: 0 quickSort #50000: 6588, STL sort #50000: 6588 quickSort #100000: 13150, STL sort #100000: 13150 quickSort #150000: 19688, STL sort #150000: 19688 quickSort #200000: 26210, STL sort #200000: 26210 Press any key to continue . . .
Too close to compare on Windows. Let's test our Unix-based Mac and have made some headway, let's see how our fastest sort compares with it. (I'm using Xcode here, no optimization):
// 250000 ints quickSort Elapsed Time: 0.074121 seconds. STL Elapsed Time: 0.015425 seconds. // 5000000 ints quickSort Elapsed Time: 0.155823 seconds. STL Elapsed Time: 0.032754 seconds. // 1000000 ints quickSort Elapsed Time: 0.326462 seconds. STL Elapsed Time: 0.068845 seconds. // 2000000 ints quickSort Elapsed Time: 0.682932 seconds. STL Elapsed Time: 0.14434 seconds.
We are now less than 5× slower than STL sort. A big improvement ...
...but wait. We have not turned optimization on in the Mac compiler. This will make both the STL and our custom sorts go as fast as possible. Let's do that (I'm in Eclipse, now, optimization on):
// 250000 ints quickSort Elapsed Time: 0.019644 seconds. STL Elapsed Time: 0.014977 seconds.. // 5000000 ints quickSort Elapsed Time: 0.041326 seconds. STL Elapsed Time: 0.031501 seconds. // 1000000 ints quickSort Elapsed Time: 0.087501 seconds. STL Elapsed Time: 0.066205 seconds. // 2000000 ints quickSort Elapsed Time: 0.181294 seconds. STL Elapsed Time: 0.138059 seconds. // 4000000 ints quickSort Elapsed Time: 0.379956 seconds. STL Elapsed Time: 0.289733 seconds.
By using a hand-made quickSort, we have pulled to within 1.3× (slower than) the STL sort, which is quite satisfying. We are writing code above all the libraries and compiler translation, yet we are getting nearly the same performance at all levels as the best that the compiler programmers can do. With some tweaking, I'll bet you can whittle this down to as good or better than STL.