Section 3 - Analysis of mergeSort

8B.3.1 Time Complexity of mergeSort

For a Big-Oh estimate of mergeSort, we have to count the number of times, worst case, that the operation must be performed. Here is the algorithm again, for reference:

 // mergeSort internal function
template <typename Comparable>
void mergeSort(Comparable array[], Comparable workingArray[], int arraySize)
{
   int rightStart;

   if (arraySize < 2)
      return;

   rightStart = arraySize/2;
   mergeSort(array, workingArray, rightStart);
   mergeSort(array + rightStart, workingArray, arraySize - rightStart);
   merge(array, workingArray, rightStart, arraySize);
}

The final merge() running time is easy to compute - it is called once, non-recursively, and there are no nested loops. A quick perusal of that function (last two pages) reveals that this has a worst-case running time of O(N) . Actually, merge() is usually called with two small arrays whose sizes, added together, are less than N, and only equal to N on the initial call. So this is a conservative upper bound. We step through each array exactly once, and most of the time, the arrays are strictly < N.

From this observation, and the fact that the above function is recursive, we can form a recursive relation (like we did in week 3 ... so long ago). If T(N) is the time our mergeSort takes to process arraySize = N elements, we have T(N) = 2T(N/2) + N. Imagine that N is a power of 2, say N = 2^p, for some integer p (for example N = 256 means p = 8). Then, after p function calls we will be at the end case where the recursion will stop and start to unwind. Let's apply the relation

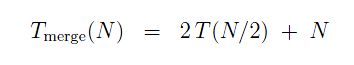
until the recursion ends. As N gets smaller, so does the right term (N) above. However, since it won't dominate the counting, I can be generous and use the original (largest) N for all the following terms causing = to be < after the first line:

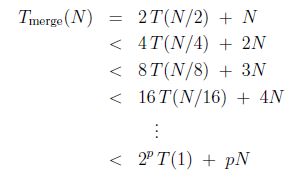
But p = log₂N and N = 2^p (by the assumption that N is a power of 2) which allows us to simplify:

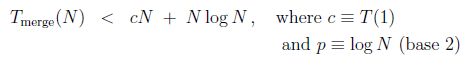
When we convert to order-of-magnitude notation, the smaller term, cN, disappears and we have:

This is what we were after - a proof that a mergeSort had worst-case NlogN time complexity.