Section 1 - mergeSort On Arrays
8B.1.1 The merge Operation
Consider two sorted arrays of compatible data types (both strings or both iTunesEntries, say). Call them a[] and b[]. We want to merge them into a single array that is sorted. Here is the picture:
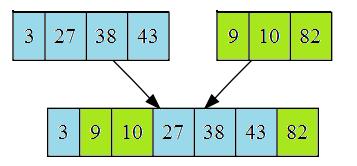
The algorithm to merge these two arrays into a third array is something that is often assigned as an exercise in a beginning programming class like CS 2A. One might not get the most efficient result, but it certainly is clear how we would proceed: start at the left side of each input array, and move gradually to the right, taking the lesser of each array as we go.
mergeSort uses this operation as its basic move. In mergeSort, the two input arrays will share the same home array, client[], with a[] populating the left portion of the client[] and b[] constituting the right-most elements of client[]. After all, there is no reason that a[] and b[] cannot really be two sub-arrays of a larger array.
We start with an array-based implementation of this operation which we call merge(). It is not the full mergeSort() function (that will take a client array) since it works on two input arrays which it assumes to be pre-sorted, and produces a third. But it does the hard work for us.
merge() will take an argument from the client, an array, client[] which contains the two input arrays. The first (left) array is assumed to be in index positions 0 through rightPos - 1. The second (right) array is assumed to be in index positions right_position through arraySize - 1. In order to make this work, we pass the two index positions, rightPos and arraySize. This makes for three reasonable parameters, client[], rightPos, and arraySize. However, we will need an internal array, working[], in order to capture the results of the merge, because we cannot mess-up the input array(s) in client[] until we have the full merge complete. Since allocating a local array will cause a resource and time drain every time merge() is called, we will allow it to be allocated outside and before the call to merge() and pass the working array in as a parameter. Nothing is sent into merge() through working[] nor is anything returned using it. It is there only to avoid constant allocation and de-allocation of a local array as merge() is called. Note that even C++ static cannot help since we don't know the size of the array this far down the function call stack.
With this intro, we are ready to see merge().
// input array 1: client[0] ... client[rightPos-1]
// input array 2: client[rightPos] ... client[ arraySize - 1]
// working[] array supplied by client to avoid local allocation
template <typename Comparable>
void merge(Comparable client[], Comparable working[],
int rightPos, int arraySize)
{
int leftPos, leftStop, rightStop, workingPos;
workingPos = leftPos = 0;
leftStop = rightPos - 1;
rightStop = arraySize - 1;
// as soon as we reach the end of either input array, stop
while(leftPos <= leftStop && rightPos <= rightStop)
if(client[leftPos] <= client[rightPos])
working[workingPos++] = client[leftPos++];
else
working[workingPos++] = client[rightPos++];
// merge is over; copy the remainder of one or the other input array
while(leftPos <= leftStop)
working[workingPos++] = client[leftPos++];
while( rightPos <= rightStop )
working[workingPos++] = client[rightPos++];
// copy back into client array
for( ; rightStop >= 0; rightStop-- )
client[rightStop] = working[rightStop];
}
The first while loop does the real work. It moves leftPos and rightPos along the two input arrays, starting them both at the bottom of their respective arrays, and moving them gradually up toward the end of those arrays. Whichever index is pointing to the smaller element gets to move forward (++) one position as we copy that smaller element into the result array working[]. This is the embodiment of a merge.
Eventually, we reach the end of one of the arrays. Once that occurs, we move on to the final while loops, one of which will be ignored, and the other will be used to copy the remainder of the unchallenged values directly into the array working[]. (This last part could be further optimized by recognizing that, at this point, we can actually copy directly into client, but it only affects the tail-end of the merge and is not worth doing unless you are trying to squeeze the last 1% of speed out of the algorithm.)
8B.1.2 mergeSort()
With merge() done and in place, we can call it from mergeSort(). mergeSort() will be a recursive function. It is very simple. We take the input array of size N and break it into two parts:
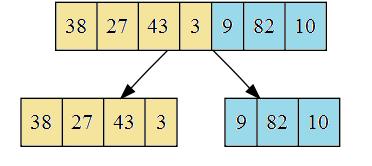
The left array is locations 0 through N/2. The right array is locations N/2 + 1 through N - 1. We recursively call mergeSort() on these two arrays (which are smaller than the original, thus allowing recursion) and we then merge() the two arrays.
// mergeSort internal function
template <typename Comparable>
void mergeSort(Comparable array[], Comparable workingArray[], int arraySize)
{
int rightStart;
if (arraySize < 2)
return;
rightStart = arraySize/2;
mergeSort(array, workingArray, rightStart);
mergeSort(array + rightStart, workingArray, arraySize - rightStart);
merge(array, workingArray, rightStart, arraySize);
}
This particular implementation puts the central element into the right sub-array, in contrast to the description and picture which puts it into the left sub-array. However, the logic is unchanged.
We can see clearly here that the array is broken into two parts and each is sorted recursively at a lower level. Then the final merge is done. One feature of this method is the extra parameter workingArray[] which is supplied by the client for the same reason that merge() takes it -- it is too costly, and tactically difficult -- to declare it locally. Since mergeSort(), in its current incarnation, is an internal method, which calls itself recursively, this is not the place to define the working array. That is done by the public driver which the ultimate client uses.
Here, finally is that public client:
template <typename Comparable>
void mergeSort(Comparable array[], int arraySize)
{
if (arraySize < 2)
return;
Comparable *working = new Comparable[arraySize];
mergeSort(array, working, arraySize);
delete[] working;
}
The working array is allocated dynamically, passed into the recursive version of mergeSort() and then released.
The dynamics of the algorithm is pictured here in a graphic that is available from Wikipedia. It represents the breaking of the larger input arrays into two smaller arrays at each level. After each smaller array is sorted recursively at a lower level, it is merged together, building up the final sorted array:
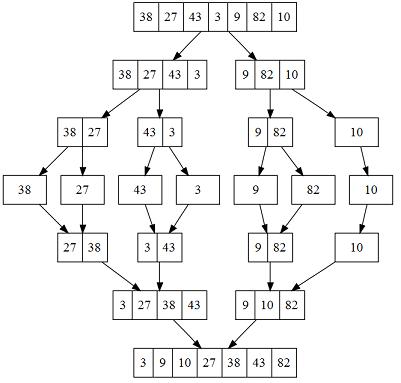
As usual, it is a mistake to try to match the big picture with the code in recursion. By its nature, recursion works by not looking deeper than the current level at any time. However, it is fun, and a little educational, to see the symbolic divide-and-conquer tactic that recursion provides.
8B.1.3 A Client
We can see the performance of mergeSort in a client. Because both mergeSort and shellSort are very fast, especially when working on primitive raw arrays, it is very hard to find a difference. But with large enough arrays, there seems to be some slight difference. As we will see, mergeSort is O(NlogN) while we noted that shellSort is O(N3/2), and hypothesized to be O(N7/6) with the right gap sequence. While seems close to N, it is still not as fast as O(NlogN) for large arrays, since no root of N, not even N1/10000 grows more slowly than logN.
With small arrays it is hard to get mergeSort to beat shellSort. However, it definitely wins as the array size gets large. Also when you are sorting large objects whose swapping takes time, mergeSort prevails even on array sizes less extreme.
First, the source.
// Comparison of merge and shell using arrays
#include <iostream>
using namespace std;
#include "Foothill_Sort.h"
#include "FHsort.h"
#include <time.h>
// --------------- main ---------------
#define ARRAY_SIZE 100000
int main()
{
int k;
int arrayOfInts[ARRAY_SIZE];
int arrayOfInts2[ARRAY_SIZE];
clock_t startTime, stopTime;
cout << "Array size: " << ARRAY_SIZE << endl;
// build an array and two vector for comparing sorts
for (k = 0; k < ARRAY_SIZE; k++)
{
arrayOfInts[k] = rand()%ARRAY_SIZE;
arrayOfInts2[k] = arrayOfInts[k];
}
startTime = clock(); // ------------------ start
// sort using shellSort sort (in FHsort.h)
shellSort1(arrayOfInts, ARRAY_SIZE);
stopTime = clock(); // ---------------------- stop
cout << "FH shellSort Elapsed Time: "
<< (double)(stopTime - startTime)/(double)CLOCKS_PER_SEC
<< " seconds." << endl;
startTime = clock(); // ------------------ start
// sort using mergeSort (in FoothillSort.h)
mergeSort(arrayOfInts2, ARRAY_SIZE);
stopTime = clock(); // ---------------------- stop
cout << "FH mergeSort Elapsed Time: "
<< (double)(stopTime - startTime)/(double)CLOCKS_PER_SEC
<< " seconds." << endl << endl;
/*
// confirming that we got the correct results on all three arrays
for (k = 0; k < ARRAY_SIZE; k+= ARRAY_SIZE/10)
{
cout << "shell #" << k << ": " << arrayOfInts[k] << ", ";
cout << "merge #" << k << ": " << arrayOfInts2[k] << endl;
}
*/
return 0;
}
Here is a result for a fast Windows machine (optimization on):
Array size: 100000 FH shellSort Elapsed Time: 0 seconds. FH mergeSort Elapsed Time: 0.009 seconds. Press any key to continue . . .
I can't even get the shellSort time to register. And due to Windows compiler constraints, we cannot allocate a fixed array larger than this, so I'll move to a Mac which is Unix-based:
Array size: 10000 FH shellSort Elapsed Time: 0.002503 seconds. FH merge Elapsed Time: 0.002075 seconds. Array size: 100000 FH shellSort Elapsed Time: 0.037261 seconds. FH merge Elapsed Time: 0.025462 seconds. Array size: 300000 FH shellSort Elapsed Time: 0.125542 seconds. FH merge Elapsed Time: 0.079844 seconds. Array size: 600000 FH shellSort Elapsed Time: 0.285059 seconds. FH merge Elapsed Time: 0.167127 seconds. Array size: 1000000 FH shellSort Elapsed Time: 0.527039 seconds. FH merge Elapsed Time: 0.288308 seconds.
mergeSort beats the standard shellSort by a factor of 2 on large arrays, which is better than even the best explicit gap-sequence shellSort. As you can see, with small arrays, there is little difference, and with really small arrays, shellSort wins.