Section 4 - Improving shellSort

8A.4.1 Why Is shellSort Faster Than insertionSort?

Now that we understand the basics of shellSort, I will change the name ONE to the more traditional gap. I call it gap because, in the early passes of the outer loop (i.e., well before the final pass where gap =1), the inner loops look like an insertionSort but with all the comparisons and upward movement happening in larger gaps than 1.

Let's assume that in an early pass of the outer loop, we have gap = 100. The two inner loops still work a lot like insertionSort, separating the group into the left unsorted part, and the right sorted part, inserting the next item into the left unsorted part. However, rather than testing the item to be inserted with every value in the left portion, we only test every 100th value. And if we have to move an element in the left unsorted part up in the array, we move it 100 positions, not 1 (because of this: a[k] = a[k - gap]). We are leaving "gaps" in our sorting logic of size 100. After that early outer loop pass (gap = 100), if we were to start at any place in the array, say position 27, and hop up the array, looking at every 100th element: 27, 127, 227, 327, 427, ... etc., it would appear that those values were sorted. Same with elements in positions 9, 109, 209, 309, etc. That's the result of gap = 100 pass in the outer loop, The loop is said to be "100-sorted".

If the array size is 1000, then the shellSort as we have it will, in the first pass of the outer loop, leave the array in a state where it is 1000/2 or 500-sorted. The next pass will make it 500/2 = 250-sorted. Then next pass it will be 125-sorted, and so on until, in the final pass it is 1-sorted, which is to say it is totally sorted. Reinforce your memory, looking at the algorithm again, with ONE replaced by gap. I have color coded the 3 loops: the outer gap loop, the middle pos-loop and inner k-loop.

// shellSort #1 -- using shell's outer loop
template <typename Comparable>
void shellSort1( FHvector<Comparable> & a )
{
   int k, pos, arraySize, gap;
   Comparable tmp;
    
   arraySize = a.size();
   for (gap = arraySize/2;  gap > 0;  gap /= 2)  // outer gap loop
      for(pos = gap ; pos < arraySize; pos++ )   // middle loop (outer of "insertion-sort")
      {
         tmp = a[pos];
         for(k = pos; k >= gap && tmp < a[k - gap]; k -= gap )   // inner loop
            a[k] = a[k - gap];
         a[k] = tmp;
   }
}

There are two important ideas that contribute to understanding why this "decreasing gap" strategy improves the speed compared to insertionSort:

1. The early phase moves out-of-place numbers very quickly toward their final positions because of the large gaps.
2. When we move from a larger gap to a smaller one, the smaller ordering does not break the previous larger ordering. That is, if the array is 100-sorted, and we then go on to the next outer loop pass to make it 50-sorted, the new movements preserve the 100-sorting.

These two properties are intuitive, but should not be taken for granted. Some thought is required, and a written proof of item 2 is needed if one wants to be rigorous.

8A.4.2 Why Is Shell's Original Outer Loop No Worse Than O(N²)

First, we need to verify that we have not made the big-oh complexity theoretically worse than quadratic. We might have, given our opening observations that we are seemingly embedding a known O(N²) algorithm inside a loop, which could only make it worse, not better. Actually, the early passes of the outer loop are faster because of fewer comparisons. For example, if the array has size 1000, and gap is 100, the middle loop (which is the outer loop in the insertion-like sort) has roughly 1000 - 100 = 900 passes, but for each of these passes, the inner loop of this insertion-like sort has at most 10 passes (1000/100). (Look at the code to confirm this; you will actually see that the inner loop has fewer than 10 passes most of the time.)

In general, for an array of size N, when we are on the outer loop pass with gap = g, the middle loop has at most N - g passes and for each of these, the inner loop has fewer than N/g passes. The worst case running time for the two inner loops on pass with gap = g is then:

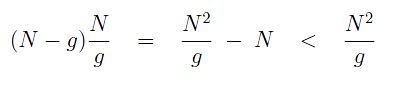
Using Shell's gap sequence:

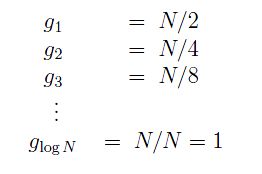
(log means log₂ in these equations.) Shell's running time is therefore, less than the sum of each outer loop's times:

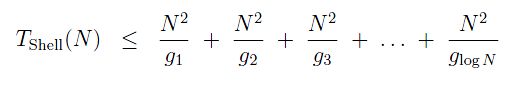
Substituting the values for each g_k and simplifying, we get:

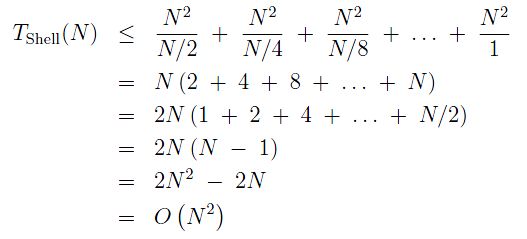
(Make sure you can justify each equality. I reserve the right to ask you to explain any of them to me on a test.)

So, the algorithm seems to be O(N²); we have not made matters worse.

8A.4.3 Why Is Shell's Original Outer Loop No Better Than O(N²)?

The idea of "halving" the gap each outer loop pass sounds good, but it is not. We saw that for random arrays, the results are excellent, but the irony is, this algorithm is still O(N²), and this bound is tight. All we have to do to prove it is tight is to find a sequence that takes the full quadratic time to sort.

Take N = some power of 2 like 128 or 1024. The gaps are then 64, 32, etc down to 1. Since all but the last gap is even, this means that the even positions never mix with the odd positions in the sorting until the final gap = 1 loop. For example, when gap is 8, then we are comparing positions k and k + 8. Also, we are moving positions from a[k-8] to a[k]. If k is an odd number so is k + 8 and k - 8 and if k is even, then the same is true when we add or subtract 8. Therefore, we have a plan to make a sequence which stays very unsorted until the final pass of outer loop, namely, gap = 1. Put the number 99 into all the even positions (0, 2, 4, 6, etc.) and the number 1 in all the odd positions (1, 3, 5, ...). So here is our original, unsorted array:

99 1 99 1 99 1 99 1 99 1 99 1 ...

When we get to the final gap pass of 1, the array is unchanged. As we know, the final pass of a shellSort is just an insertionSort. This particular sequence is not going to be fun for insertionSort. Every time we hit a 1 in pos, we have to do pos/2 compares to find its correct place in the left sequence since there are pos/2 99s we have to move past. This means that the inner loop uses pos/2 passes when it sees a 1, which is half the time. The number of explicit loop passes then is the sum of all terms pos/2 whenever pos is odd, namely:

1/2 + 3/2 + 5/2 + ... + (N-1)/2

With a little rearrangement and math this is:

(1/2) [ 1 + 3 + 5 + ... + (N-1) ]

= (1/2) [N/2]²

= Ω(N²)

Or, to put it a little more melodramatically, our worst fears have been confirmed. With all the bad-press, though, please note that on random arrays, Shell's gap sequence still works 10 to 200 times faster than insertionSorts, as we have demonstrated empirically.

8A.4.4 Hibbard's Choice of Gaps

Gaps are often pre-computed and stored in an array. For example, Shell's gaps could be computed from lowest to highest, as follows:

1, 2, 4, 8, 16, 32, 64, ..., 2^k, ...

until we reach the size of the array. This is slightly different from starting with the array and dividing by two, but it gives the same results and has the advantage of not requiring computation. Using this idea, we can now start to ask what are good gap sequences in this form (since we know Shell's isn't optimal).

There are some very good sets of gaps that avoid the problem with Shell's original choice. The easiest to code using a formula, and quite good, is one by Hibbard:

1, 3, 7, 15, ..., 2^k - 1, ...

Well this is practically the same as Shell's! But the big difference is that these numbers do not produce sub-arrays that do not mix until the final gap pass as Shell's did. The reason, speaking mathematically, is that each pair of neighboring gap values in this sequence is relatively prime, while the neighboring gaps in Shell's sequence were as far from relatively prime as one can get. Intuitively, you might imagine that two relatively prime gaps will result in less overlap of work in their respective outer loop passes, thus doing more work in the same amount of time. This is purely conjecture, but it is how I like to think of it. The real proof (which we shall not discuss due to its technical complexity) hinges on the fact that two relatively prime gaps, g_k and g_k+1, say, once used to g_k-sort and g_k+1-sort the same array, give an upper bound (in terms of g_k and g_k+1) on how many elements to the left of a position, p, can be larger than a[p]. Recall that the more larger elements to the left of a[p], the more compares and moves we have to make when we go to insert a[p] in the growing sorted left sub-list. That means that the next gap sort pass, g_k+2, will find its insertion positions more quickly. The proof establishes a formula for the upper bound , so we have an upper limit on how bad the inner loop will be for all subsequent gap loop passes after g_k and g_k+1. When you use that formula and add it up for all the gaps in Hibbard's sequence, you find that shellSort with the Hibbard sequence is O(N^3/2), which is finally better than quadratic.

This bound is not necessarily tight for Hibbard sequence, and it is possible someone will prove that there is actually a lower bound.

8A.4.5 Other Gap Choices

There are other gap choices for shellSort, and over the years, mathematicians and computer scientists have come up with gap sequences that are shown to work better than even Hibbard's. For our purposes, though, we have reached the conceptual end of this topic. You can research gap sequences that are purported to give good running times and try them out.