Section 1 - insertionSort

8A.1.1 Idea Behind insertionSort

The insertionSort is not the sharpest knife in the drawer. Nor is it the sharpest pencil in the box. It's nothing to write home about and it's not the bees' knees. In other words, it is O(N²), no better, theoretically, than the bubble sort. So why do we study it? Several reasons:

1. It allows us to sort elements as they come in to us, without knowing the ultimate size of the input array.
2. It has O(N) performance on nearly sorted arrays and this is very useful in many applications.
3. It is extremely easy to code.
4. shellSort, which is much faster on random arrays, is a minor modification of the insertionSort, making insertionSort a good stepping stone to this faster algorithm.
5. For small arrays of size < 20 or so, it beats most other sorts, even quickSort and mergeSort (coming up), and we will need this property next week.

A typical insertionSort implementation works using a double loop. An outer loop starts from position 1and moves up until the end of the input array is reached. After each pass of the outer loop, the "left portion" of the list is completely sorted. As the outer loop progresses, this "left" portion gradually grows until it becomes the full input array, meaning that by the last pass of the outer loop the "left", sorted, portion is everything.

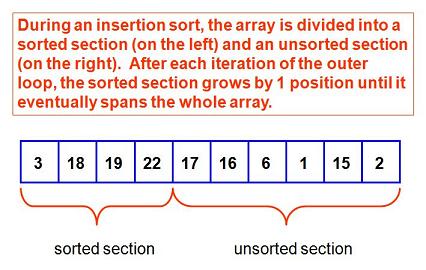
To visualize this, imagine that we are doing one pass of our outer loop: we are supposing that we have completed three loop passes and are now considering position four:

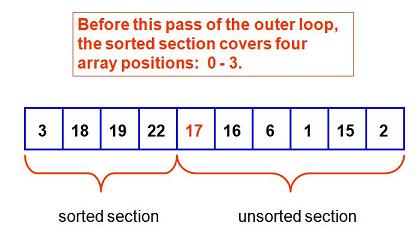
Since we have had three passes already, we have managed to sort everything to the left of position four before we begin this next pass. There is a 17 in array position four. Here is the picture. Now we plan to place the 17 into the sorted section, thus growing the sorted portion by one position:

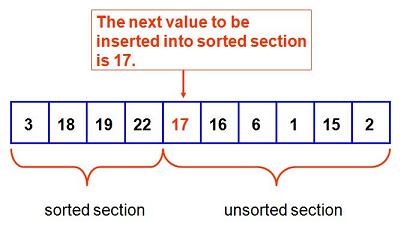
This takes us into an inner loop, which searches the sorted position from right-to-left until the proper place for the new item, 17, is found:

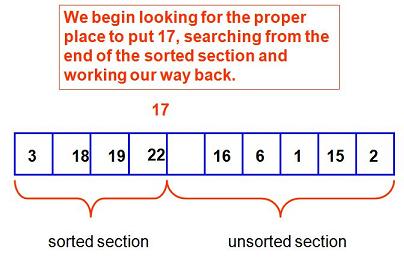
Our inner loop keeps looking, and as it does, it moves each element one item to the right, making room for the 17, when the proper array location is found:

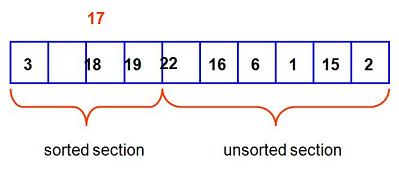
Finally, we find the correct position for 17 and place it there. Now we have completed this pass of the outer loop, causing the sorted section to grow from four elements to five elements. The "left", sorted, section, has grown, as promised. We then go on to the next pass of the outer loop:

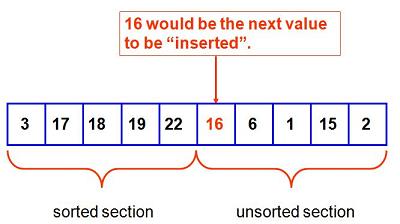
8A.1.2 insertionSort Code

Every sort function has a similar interface, or "driver". It will take an array or vector as an input parameter, and it usually returns with that array, sorted. Sometimes, the driver takes two arrays, an input and an output -- this, in case the client wants the input array unmodified. However, normally, the algorithms assume the client wants the input array rearranged, and if for some reason it doesn't, the client can do what it needs to to save a copy of the input array.

template <typename Comparable>
void insertionSort( FHvector<Comparable> & a )
{
   int k, pos, arraySize;
   Comparable tmp;
    
   arraySize = a.size();
   for(pos = 1; pos < arraySize; pos++ )
   {
      tmp = a[pos];
      for(k = pos; k > 0 && tmp < a[k-1]; k-- )
         a[k] = a[k-1];
      a[k] = tmp;
   }
}

Let's test the insertionSort against the bubble sort using straight arrays.This code used FHvector as its input array type. This means that this template file must #include "FHvector.h" and the client must pass it an FHvector object. However, you can modify it in two ways to make it independent of this requirement:

1. Change FHvector to vector, thereby shifting the requirement to the STL vector usage.
2. Pass an array, rather than a vector, in which case you must expand the parameter list to include an int arraySize.

To compare this with our bubble sort, I want to use the same driver as we did for that one, and this was an array, not a vector, interface. Therefore, let's actually show option 2:

template <typename Comparable>
void insertionSort(Comparable array[], int arraySize)
{
   int k, pos;
   Comparable tmp;

   for(pos = 1; pos < arraySize; pos++ )
   {
      tmp = array[pos];
      for(k = pos; k > 0 && tmp < array[k-1]; k-- )
         array[k] = array[k-1];
      array[k] = tmp;
   }
}

Let's test the insertionSort against the bubble sort using straight arrays.

// Comparison of bubble and insertionSort algorithms
#include <iostream>
using namespace std;
#include "Foothill_Sort.h"
#include <time.h>

// --------------- main ---------------
#define ARRAY_SIZE 50000

int main()
{
   int k;
   int arrayOfInts[ARRAY_SIZE];
   int arrayOfInts2[ARRAY_SIZE];

   // build two arrays for comparing sorts
   for (k = 0; k < ARRAY_SIZE; k++)
      arrayOfInts2[k] = arrayOfInts[k] = rand()%ARRAY_SIZE;

   clock_t startTime, stopTime;
   startTime = clock();  // ------------------ start 

   // sort using a home made bubble sort (in Foothill_Sort.h)
   arraySort(arrayOfInts, ARRAY_SIZE);

   stopTime = clock();  // ---------------------- stop
   cout << "\nAlgorithm Elapsed Time: " 
      << (double)(stopTime - startTime)/(double)CLOCKS_PER_SEC 
      << " seconds." << endl << endl;

   startTime = clock();  // ------------------ start 

   // sort using an insertionSort (also in Foothill_Sort.h)
   insertionSort(arrayOfInts2, ARRAY_SIZE);
   stopTime = clock();  // ---------------------- stop

   cout << "\nAlgorithm Elapsed Time: " 
      << (double)(stopTime - startTime)/(double)CLOCKS_PER_SEC 
      << " seconds." << endl << endl;

   for (k = 0; k < ARRAY_SIZE; k+= ARRAY_SIZE/20)
   {
      cout << "bubble #" << k << ": " << arrayOfInts[k] << ", ";
      cout << "insertion #" << k << ": " << arrayOfInts2[k] << endl;
   }
   return 0; 
}

Here is the output, which shows something interesting:

Algorithm Elapsed Time: 3.183 seconds.


Algorithm Elapsed Time: 0.348 seconds.

bubble #0: 0, insertion #0: 0
bubble #2500: 1653, insertion #2500: 1653
bubble #5000: 3318, insertion #5000: 3318
bubble #7500: 4974, insertion #7500: 4974

[snip]

Press any key to continue . . .

The insertionSort works and is 10× as fast as the bubble sort. I claimed that time complexity is n-squared for both, and below I'll prove that. So why is the insertionSort so much faster than the bubble sort? Is the claim about N² time complexity wrong? No. We have to keep a clear head about what big-oh means. It is not a statement about which of two algorithms will be faster on a specific data set. Rather, it is a statement about how running times will increase, in general, if the number of elements, N, on which the algorithm acts, increases. The statement that both algorithms are O(N²) means that, for random data sets, if we double N, the time should quadruple. If we triple it, the time should increase by a factor of 9. Don't forget this as you go out into the world. It is embarrassing to make false claims (or bets) about which algorithm will give an absolute faster time based on time complexity, alone.

Let's demonstrate this concept. Double N from 50,000 to 100,000 ints and compare the results with those above:

// 100,000 ints
/* --------- output -----------


Algorithm Elapsed Time: 12.979 seconds.


Algorithm Elapsed Time: 1.389 seconds.

[snip]

Press any key to continue . . .

Taking ratios of the corresponding times, and taking the nearest int, we find:

12.979/3.192 = 4

1.389/0.348 = 4

Aha. This is quadratic - in both cases.

8A.1.3 Time Complexity of insertionSort

If we unwind the loop, we can easily compute the big-oh estimate for insertionSort. We assume the worst case, that is, the inner loop ends by letting k travel all the way down to 0. Then, letting C be the constant-time body (and comparison test) of the inner loop, we find the following:

Worst-Case-Time = C (1 + 2 + 3 + ... + (N-1)) = C (N-1)N/2

Therefore, insertionSort = O(N²).

Also, like bubble sort, insertionSort will complete processing a previously sorted (or nearly sorted) array in linear time.

• In the case of bubble sort, the reason it is linear is that we will escape from the outer loop after one or two passes, once the inner boolean flag (which is called "sorted" in the function I presented in the first week), is true. This means the time will be CN or 2CN or even 3CN, if the array is sorted after 1, 2 or even 3 passes, due to nearly sorted input. All of these cases are O(N).
• In the case of insertionSort, the reason it is linear is that each inner loop ends in constant time as the position for tmp is found on the first (or second or third) test, obviating the need for the bulk of the inner loop. Thus, we get N-1 (or maybe 2(N-1) or 3(N-1)) terms in the above expression, which results in a sum of C(N-1) (or maybe 3(N-1) which is O(N)).