Week 7B Heap Sort

Section 1 - orderHeap() Performance

7B.1.1 Facts About Perfect Trees of Height h

A perfect binary tree, as you recall, is one in which each of its node's two subtrees are exactly the same height. This is like a complete tree in which the lowest level is completely filled out. Here is an example of a perfect binary tree (PBT) of height 6:

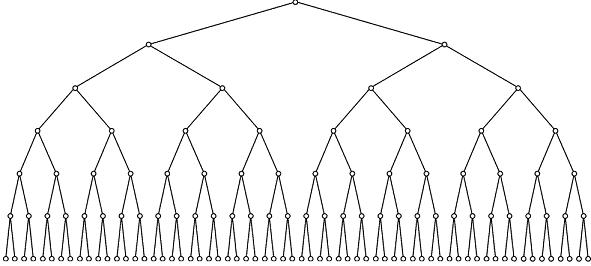
A PBT clearly has 2^M - 1 nodes, where M is some integer. Some thought will reveal that M-1 is the height of the PBT. Let's explore this idea.

The height of a PBT, which we'll call h, determines the number of nodes, N(and vice versa). For example, it is easily seen that:

The number of nodes, N, in a PBT of height h is 2^h+1 - 1.
The height of a PBT with N nodes is log(N+1) - 1,

As usual, log is assumed to be log₂.

To cement these two bullet points, we note that in the picture above, h = 6 and N = 2⁷ - 1 = 127.

We will find it useful to compute the sum of the heights of every node in a PBT. For example the height of the root node in the above tree is 6 (which is no surprise since the tree has height 6). That node has two children, each of which have height 5. Each of those nodes has two children which have height 4. If we add the heights we would get a sum:

sum of heights in above tree = 6 + 5 + 5 + 4 + 4 + 4 + 4 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + ... (it gets long)

We want to figure out what this number is. It's a good mathematical exercise to at least think about it, and we will do it in a way that is a little different from the text. Let's symbolize the sum of the heights in a PBT tree whose height is h by the notation S_h.We start with a very simple recursive relation:

Lemma: S_h+1= S_h + (2^h+1 - 1)

Proof: Consider a PBT of height h whose heights sum to S_h. We now create a new PBT of height h + 1 by adding a bottom row of nodes - two children for each previous leaf on the tree with height h. What is the sum of the heights of this larger tree? The newly added bottom row of nodes will add nothing, because they are all leafs, having height 0. Meanwhile, each node in the original tree had some height, x, before we added the bottom row, and now its height in the supersized tree will be x + 1. So for every node in the original tree, we change its height in the new tree by adding 1. Since there are exactly 2^h+1 - 1 nodes in the original tree, we have added that many 1s when summing the heights in the new tree, giving the relation S_h+1 = S_h + (2^h+1 - 1), as promised.

Now we come to the theorem that will give us the formula for the sum of the heights in a perfect binary tree.

Theorem: S_h= (2^h+1 - 1) - (h + 1)

Proof: We use induction. For h = 0, it is immediately seen that the S₁= 1 and S₀= 0, so we confirm the relation directly

S₀ = 0

while

(2¹ - 1) - (0 + 1) = 1 - 1 = 0

Next we use recursion. Assume that relation is true for h-1 and we prove it for h. From the lemma we have:

S_h= S_h-1 + (2^h - 1)

and by recursion, we can replace S_hby its result:

S_h-1= (2^h - 1) - h

Plugging this result into the equation above, we get:

S_h= (2^h - 1) - h + (2^h - 1)

2^h + 2^h = 2^h+1 and by rearranging using simple arithmetic, we get the result:

S_h= (2^h+1 - 1) - (h + 1)

7B.1.2 Performance of orderHeap()

We didn't do this last computation for our health. It is going to give us a significant result.

The private method orderHeap() which is used by the constructor that takes a vector, has an easy-to-compute upper bound. Consider a tree with N nodes. The main function orderHeap() has a loop of size N/2, and this loop calls a function percolateDown() which, worst case, has a loop that executes logN times (why? You should know this.). That means orderHeap() is O(NlogN). However we can do better. [Note - we don't actually have to do better in order to get a great result for our heap sort on the next page, but we may as well take credit for speed of orderHeap() - no reason not advertize the faster time if we are really achieving it.]

In this analysis, we gave a worst case estimate. We treated each call to percolateDown() as if it had O(logN) time complexity. However, when you think about it, we will be calling percolateDown() more often near the bottom of the tree than near the top (simply because there are more nodes near the bottom than there are near the top). Calling it closer to the bottom costs less because we don't have as far to percolate down. Furthermore, it is not random. We will call the method systematically, so we can actually unwind the function call and consider the inside of percolateDown() as though it was directly in orderHeap(). When we do that, we see that we enter the percolate loop starting at node position N/2 which is way down at level 1, and then slowly work our way up to the root of the tree.

Here is the body of the loop that we do N/2 times:

   {
      child = 2 * hole;
      // if 2 children, get the lesser of the two
      if( child != mSize && mArray[child + 1] < mArray[child] )
         child++;
      if( mArray[child] < tmp )
         mArray[hole] = mArray[child];
      else
         break;
   }
   mArray[hole] = tmp;

So, while we are on level 1 (i.e., the nodes with height 1, one level up from the bottom), there is only one level below us -- level 0. And in that case the loop terminates, worst case, after one pass. We therefore execute the body (a fixed O(1) operation) at most once for each node at level 1.

As the client (orderHeap()) loop backs-up each time, it will repeat this for all nodes in level 1, eventually coming to the next higher level, level 2. Now, for each node on level 2, we will enter the above loop and do it, at most, twice, once at level 2 and possible have to let the hole descend to level 1. This happens for all the nodes on level 2, and eventually we step up to level 3. Each node in level 3 executes the body of the above loop at most 3 times, as hole descends, worse case, to the bottom.

You should see the pattern. For each node, we will execute an O(1) set of instructions at most the number of times equal to its height. This means that if we add up the heights of every node in the tree, that's the number of times we will execute the constant time body of the innermost loop. So, we need a bound on the sum of the heights of nodes in a complete binary tree.

It so happens that we solved nearly that problem in the last section. There we obtained a bound for the sum of the heights of a PBT. We found that:

S_h= (2^h+1 - 1) - (h + 1)

Since a complete binary tree is smaller than the PBT which contains it, we can use this as an upper bound for our current situation.

What have we discovered? That O( orderHeap() ) = S_h= (2^h+1 - 1) - (h + 1), where (2^h+1 - 1) is just N', the number of elements in the perfect binary tree that surrounds the bin heap. The PBT that holds the binary heap has size, at most, twice the binary heap (why?) So N' < 2N. We have something that looks like this:

O( orderHeap() ) = 2N - (h + 1) = N

Don't forget that neither multiplication by constants, nor subtraction or addition by smaller values, will change big-oh. Therefore, we see that the vector-parameter constructor that calls orderHeap() is an O(N) algorithm for placing a randomly shuffled vector into a binary min (or max) heap.