Section 3 - Remove and Percolate Down
7A.3.1 "Percolate Down"
Removing an item consists of a trivial step, followed by a percolate step. The highest priority item (min value) is at the root of the tree. We copy that to our return value. Next, we have to adjust the tree because that leaves an empty location which we must fill. The idea is simple:
- Place the last item in the underlying vector -- i.e. the right-most non-empty node in the bottom row -- into the root. We'll call this the moved-item.
- The moved-item is now in the tree in two places. Remove it from its original place in the bottom row by decrementing the mSize (mSize tells us where the real data lives -- and where it stops living).
- Most likely, the root is not the correct place for the moved-item. If it is (i.e., its key is) greater than either of its children this violates the binary min-heap ordering property. If that's the case, we swap it with its lesser child (the one with the smaller key).
- Repeat the compare-and-swap of the previous step until the copied item finds a position in which it is smaller than both its children.
The last two steps constitute a "percolate down" operation. Because percolate down will be useful elsewhere, we give it a private helper method in which to live. First, I'll show you that, then I'll demonstrate the remove() procedure in detail.
template <class Comparable>
void FHbinHeap<Comparable>::percolateDown(int hole)
{
int child;
Comparable tmp;
for( tmp = mArray[hole]; 2 * hole <= mSize; hole = child )
{
child = 2 * hole;
// if 2 children, get the lesser of the two
if( child < mSize && mArray[child + 1] < mArray[child] )
child++;
if( mArray[child] < tmp )
mArray[hole] = mArray[child];
else
break;
}
mArray[hole] = tmp;
}
This method takes an int, the vector index, representing the tree node that we want to percolate down into its proper place. To work, the algorithm assumes that the heap was otherwise correctly heap-ordered prior to placing a value, which could be anything, into position hole. Then, it compares hole to its children and moves it down, if necessary (as described in the text before this code).
If the code does not reveal itself to you by reading directly, here is some commentary:
- We copy the data from hole into a tmp variable. This is so we don't really have to swap it with either of its children. Like in percolate up, we will simply copy children up until we find the place to put tmp. Position hole will "percolate down" the tree.
-
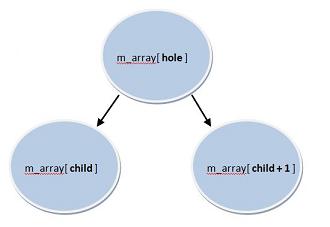 Next, we check that node hole has at least a left child. This will be true as long as 2 * hole <= mSize. Therefore, we use this as our loop termination expression. (If node hole has no children, we have found a place to put tmp and we are done.)
Next, we check that node hole has at least a left child. This will be true as long as 2 * hole <= mSize. Therefore, we use this as our loop termination expression. (If node hole has no children, we have found a place to put tmp and we are done.) - We assign child the index of hole's left child: child = 2 * hole.
- We now want to know if this is node hole's only child. So we ask whether child != mSize. If so, node child has a sibling at child+1, and we compare the data in child with that of its sibling (mArray[child + 1] < mArray[child]). The code in that if statement adjusts child, if necessary, to point to the lesser of the two siblings (node hole's two children).
- After step 4, we can compare tmp with node child (at this point child is no longer necessarily the left child, but is the lesser of the two children). If tmp is smaller or equal to the data in position child, we are done. If tmp is not smaller, we copy child's data up to its parent, hole, and move down one level by making child our new hole. We repeat steps 2-5.
7A.3.2 remove()
We are now ready to show remove(), which lets percolateDown() do the hard work.
template <class Comparable>
Comparable & FHbinHeap<Comparable>::remove()
{
static Comparable minObject;
if( empty() )
throw HeapEmptyException();
minObject = mArray[1];
mArray[1] = mArray[mSize--];
percolateDown(1);
return minObject;
}
We will return the found data as a functional return. However, to keep the execution efficient the code uses a reference type for the return type. It then returns the value stored in a static local variable. Such a plan results in a variable that is kept in a global memory area and so does not have to be re-allocated every time the function is invoked. Also, the return operation does not require the handling of a potentially large Comparable object -- only the reference, i.e., a pointer, will be returned no matter how large Comparable is.
We will be throwing a custom exception if the heap is empty. Its definition is found in the prototype already displayed.
Otherwise, all is well, and we move the data into minObject for return. Then we prepare for the percolate down as follows:
- Place the last item in the underlying vector -- i.e. the right-most non-empty node in the bottom row -- into the root. We'll call this the moved-item.
- The moved-item is now in the tree in two places. Remove it from its original place in the bottom row by decrementing the mSize (mSize tells us where the real data lives and where it stops living).
(These are just the first two of the four steps we talked about at the top of this page.)
We now let percolateDown() work starting at the root, hole = 1.
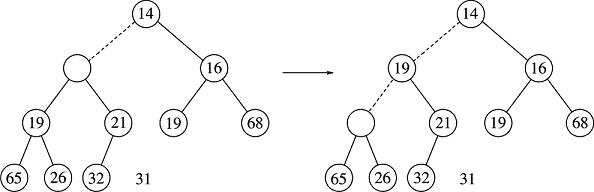
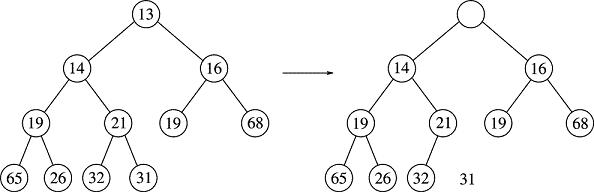
In the following picture, we remove 13 from the binary heap. This leaves an unused node at the root, which we fill with the last item (31) in the tree (conceptually, not literally). This is the prep before calling percolateDown():
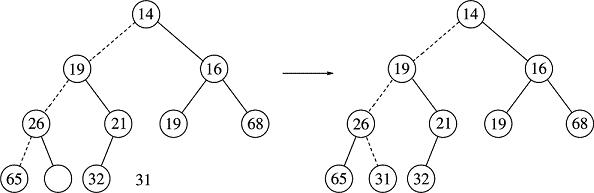
Within percolateDown() the hole quickly moves down (imagine 31 in the hole positions, even though it is really aside, safely tucked away in tmp):