Section 2 - Implementing Binary Heaps
7A.2.1 FHbinHeap Class Overview
Let's dive right into the class prototype. It is very sparse and requires no embedded node types, making it one of the simplest, if not the simplest ADT we have so far undertaken. We use the type name Comparable -- rather than Object -- to remind us that whatever type the client provides must implement operator<().
// ---------------------- FHbinHeap Prototype --------------------------
template <class Comparable>
class FHbinHeap
{
static const int INIT_CAPACITY = 64; // perfect tree of size 63
private:
FHvector<Comparable> mArray;
int mSize;
int mCapacity;
public:
FHbinHeap(int capacity = INIT_CAPACITY);
FHbinHeap(const FHvector<Comparable> & items );
bool empty() const { return mSize == 0; }
void makeEmpty() { mSize = 0; };
void insert(const Comparable & x);
Comparable & remove();
int size() const { return mSize; }
// for exception throwing
class HeapEmptyException { };
private:
void buildHeap();
void percolateDown( int hole );
};
As our previous discussion suggested, we use a simple vector to store data. Although it may have no significant utility, I chose to initialize the size of the vector to be one that can, if filled, hold a perfect tree. Now, a perfect tree has size 2N - 1, for some integer N, but remember that we are not going to use location 0, so we'll need a vector having size 2N to hold a perfect tree of size 2N - 1, exactly. Again, you can choose any initial value and not concern yourself with perfect trees. The only methods that involve this added restriction are the constructors.
The default constructor also accepts a suggested initial size from the user, bumping the value to INIT_CAPACITY, if it is too small, and likewise bumping it to the next power-of-2 even if it is larger than the INIT_CAPACITY.
template <class Comparable>
FHbinHeap<Comparable>::FHbinHeap(int capacity)
{
// choose a capacity that is exactly 2^N - 1 for some N (esthetic)
// which leads to mCapacity 2^N, internally -- user asks for 127, we
// reserve 128, if they want 128, we have to reserve 256.
for (mCapacity = INIT_CAPACITY;
mCapacity <= capacity;
mCapacity = 2 * mCapacity
)
{
if (mCapacity < 0)
{
mCapacity = INIT_CAPACITY; // give up - overflow
break;
}
}
mArray.resize(mCapacity);
makeEmpty();
}
makeEmpty() doesn't do much - we can almost do without it here in the constructor, but it is included for the client's use. You'll see it in-line, in class prototype.
The second constructor which takes an unsorted vector, will be discussed after we study remove() and insert().

7A.2.2 insert() and "Percolate Up"
insert() demonstrates the use of the computational trick (parent → k/2, children → 2*k and 2*k + 1) which dominates all the algorithms in this ADT. First, we'll display it, then discuss it.
template <class Comparable>
void FHbinHeap<Comparable>::insert(const Comparable & x)
{
int hole;
if( mSize == mCapacity - 1 )
{
mCapacity = 2 * mCapacity;
mArray.resize(mCapacity);
}
// percolate up
hole = ++mSize;
for( ; hole > 1 && x < mArray[hole/2]; hole /= 2 )
mArray[hole] = mArray[hole/2];
mArray[hole] = x;
}
Reading from top to bottom, we come across the easily-understood first block that resizes the underlying vector, mArray, if it has become full. Since we initially constructed the binary heap to have a perfect-tree-sized mArray, doubling will automatically preserve this (frivolous?) property at no extra expense.
Next, we place the new item into the tree using a technique called "percolate up". Because of the complete tree property (see the diagrams on the last page) we know that wherever the old tree ended (in the last, incomplete, row of the complete tree structure, for example) the newly inserted item will extend this bottom row by one. The technique for insertion then is as follows:
- Put the item to be inserted into the next available location of the tree, i.e., position ++mSize. This extends the final row by one, keeping the tree complete.
- Most likely, this is not the correct place for the new item. If it is smaller than its parent, for example, this violates the binary min-heap ordering property. If that's the case, we swap it with its parent.
- Repeat the compare-and-swap of the previous step until the newly inserted item finds a position in which it is not smaller than its parent. (This loop is called "percolate up".)
Computing its parent is so easy because that can be found at position k/2, and this is reflected in the algorithm. While the three steps discuss swapping, we really don't have to swap, nor do we actually have to put x into the next available location to start things off. Rather, we just shift old parents down to child positions until we find the correct place for the new item, x, and then place x into the location of final copied parent.
To demonstrate this, we insert 14 into the following tree:
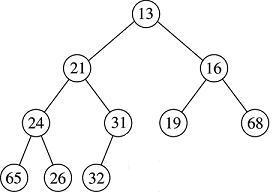
We (conceptually) place 14 into the next available location to the right of 32 in the bottom row, then we start to percolate up until it finds its proper place. First we swap with its parent, 31:
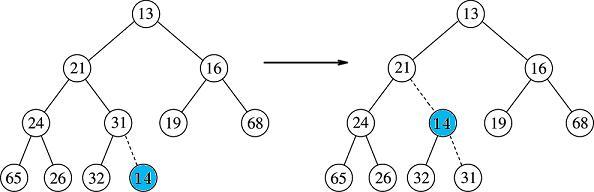
Next, we swap with its new parent 21:
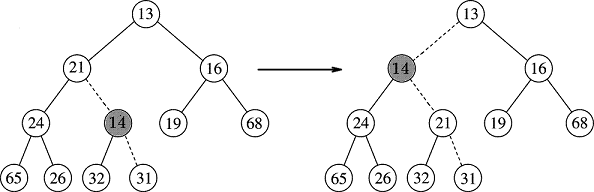
At this point, 14 > 13, its latest parent, so we are done. In reality, we will not really place 14 into the tree until after we have found the correct position, so the swaps are conceptual rather than actual.