Section 2 - Quadratic Probing

6B.2.1 Quadratic Probing

The problem with linear probing was the tendency for clustering. This can be eliminated or reduced if we don't store the collided data in the very next available location, but instead skip some locations. To decide exactly which locations to try, we now introduce a probing function f(k). Hashing proceeds as follows:

• We try to hash into a location at position hash(x).
• If it is occupied we try the location at position hash(x) + f(1).
• If that is occupied we try hash(x) + f(2). If that is occupied, we try hash(x) + f(3).
• Continue until you find a vacant location.

In linear probing, the probing function was

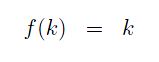
That caused clustering problems. In quadratic probing we use the function

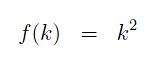
Thus, if hash(x) = 15, we will try the following locations:

15, 16, 19, 24, 31, ...

Except for the first attempt, 16, the probes skip several locations each iteration. This removes the main clustering problem of linear probing. Furthermore, notice that if a new hash maps directly into, say, location 24 on its first attempt, the very next probe for that operation will be 25, which is not occupied (at least not by any data that started from 15, 16 or 19). So collisions with the secondary nodes do not require lots of future probes.

However, that's not to say that collisions are still not a potential problem. If several keys map into 15, then the sequence of locations shown above will have to be traversed until a free location is found. This kind of clustering is called secondary clustering, and is addressed using the double hashing technique which I mentioned (but did not describe). Apparently, quadratic probing without double hashing does a fine job in most situations, so it can be applied as is.

6B.2.2 Fast Math for Quadratic Probing

We use a simple observation to avoid actually doing a multiplication for quadratic probing. First, look at a general idea for probing until we find an empty location:

   int hashIndex = myHash(x);

   for ( k = 1, index = hashIndex;  mArray[index].state != EMPTY;  k++ )
   {
      index = hashIndex + k*k;  
      if ( index >= mTableSize )
         index -= mTableSize;
   }

This is the brute force way of doing quadratic probing. However, look at the numbers we are adding to the hashIndex each time:

   index = hashIndex + 1
   index = hashIndex + 4
   index = hashIndex + 9
   index = hashIndex + 16
   ...

Since we know (from some math class) that k² = (k-1)² + kth odd number, we can write the squares like this:

   index = hashIndex + 1
   index = hashIndex + 1 + 3 
   index = hashIndex + 4 + 5
   index = hashIndex + 9 + 7

Next, instead of adding to hashIndex each time, add to the last index value

   index = hashIndex
   index = index + 1
   index = index + 3 
   index = index + 5
   index = index + 7

We are almost there. Call the number on the right the kth odd number, (for obvious reason .. 1, 3, 5, 7, etc.) we see we are just adding 2 to the last kth odd number to get the k+1st odd number:

   index = hashIndex
   
   kthOddNum = 1
   index += kthOddNum
   
   kthOddNum +=2
   index += kthOddNum
   
   kthOddNum +=2
   index += kthOddNum
   
   kthOddNum +=2
   index += kthOddNum

We will use the above short-cut in the following general algorithm that probes quadratically. It involves two additions for each loop test.

template <class Object>
int FHhashQP<Object>::findPos( const Object & x ) const
{
   int kthOddNum = 1;
   int index = myHash(x);

   while ( mArray[index].state != EMPTY
      && mArray[index].data != x )
   {
      index += kthOddNum;  // k squared = (k-1) squared + kth odd #
      kthOddNum += 2;   // compute next odd #
      if ( index >= mTableSize )
         index -= mTableSize;
   }
   return index;
}

This method, then, will return the next available location -- or else it will return the location with x in it -- for our trio of quadratic methods, contains(), insert() and remove(). It makes use of the implied members mArray (which is a vector) and mTableSize. We also get a peek at the name of our next class, FHhashQP -- QP for quadratic probing.

Oh, you are wondering why this algorithm seems so confident that it will not get stuck in an infinite loop. It is certain that it will find an empty location or the x object being hashed. I wonder why it is such a confident function? There is grounds for its hubris. We see this next.

6B.2.3.5 Load Factor for Quadratic Probing

There is a little theorem that you can find a proof of in the text of any reputable data structure reference. It says that

Theorem

If the load factor < 0.5 in an open addressing hash table (of prime size, as always), then we are guaranteed to find an empty location using quadratic probing.

Before accepting this idea, let's see why it does not hold for hash tables with larger load factors. For example, lets try this: a hash table of size seven, with four active locations:

Try to hash the number 9 into this table, quadratically. I'll wait.

Can't do it, can you? What's the load factor? Now take any one of these numbers out of the table and you will be able to hash 9 (or any other element) into it. This is not a proof that a load factor of < .5 guarantees successful quadratic hashing, but it is a proof that you can't go much past .5 and expect to have success.

So, the take-away from this theorem is that we should set our MAX_LAMBDA to 0.49 (to avoid any boundary case round-off error), and thus ensure that we will always find our data, x, or else hit an empty location in which we can store it. With a load factor < .5 we can confidently use the above method, findPos(), in our three musketeers, insert(), remove() and contains().