Section 2 - Hashing Functions

6A.2.1 ints Modulo Table Size

Let's say the key field of our data record is of int type. The simplest, fastest, and sometimes the most evenly distributed hash function is just:

hash( key ) = key % P

where P is the table size. If we choose a table size which is prime, this almost always has the properties we desire. Of course, if there is some freak run of keys like 20P + 4, 891P + 4, 1billionP + 4, 79384P + 4, etc. then bucket 4 will see a lot of business while his neighbors go broke. But if you expect certain multiples of some prime, P, you would pick a different prime table size, Q.

6A.2.2 strings Part 1: Radix 26

In order for the hash function to distribute over the entire table size -- or any table size -- we want it to generate numbers that run the range between 0 and P-1 evenly. Because we will equalize everything by using % P at the end of our computation, we can go higher -- much higher -- than P. So, how can we do this? With strings, the answer is more complicated that it was with ints. Also, simple ideas like adding the ascii values won't work.

The truth is, every application uses a different hash function because of its unique needs. I read recently about a case in which someone needed a hash function whose keys were expected to be email address strings and whose output int had to be a value between 0 and 255. Also, it had to be fast, so no multiplication was allowed. The answer involved simulated multiplications and divisions (shifts << and >>, for example) and bitwise masks of the characters. This is typical of the kind of solution that you'll have to craft. However, even this solution is based on the same basic idea: using a radix of 27, 33 or 37, and interpreting the string as a number with that radix.

To understand the idea, first look at something you should know well - hexadecimal. Here the radix is 16, and the numerals are 0, 1, 2, ... , A, B, C, D, E and F. Every String which represents a hex number looks something like this:

F001E9

We turn this into an int we can understand (i.e., a number with radix 10) by multiplying each digit by the appropriate power of 16:

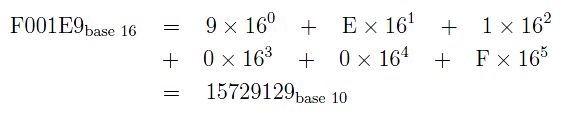
As base 16 numbers come to us, we convert them to decimal by expanding them from their radix (16) into a base 10 number. If they are random, coming in, the base 10 result will naturally be random -- because we really are not changing the number -- just representing it in a different radix (10).

A string can be thought of as a number in a different radix: If it only contains capital letters, it would be radix 26. This would give us a similarly valid technique for generating a hash function. Considering A as 0, B as 1, C as 2, etc. the String "DAD" would be a base-26 representation of the number:

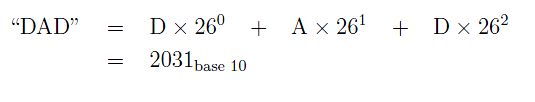
The double quotes around "DAD" mean that this is the base 26 representation, by agreement. This is basically what the hash function is, and you could use it with limited success as is.

6A.2.3 strings Part 2: Pseudo Radix 37

The question is "what do we do with lower case letters, spaces, numerals and special symbols?". All of this can be handled in a single stroke by using the ascii codes for the characters as the digit value. What radix should we use? We could keep it at 26, and it would not be terrible. This is no longer a true base 26 number because there are more digits (about 70+) than the radix value (26), so I call it a pseudo-radix. It turns out that it does not matter - we are not trying to preserve the purity of a number in a different base, but rather, the property of random and equal distribution of numbers. The radices that are commonly used are 37, 31 or 33. Contrary to some "experts" on the web, the radix does not have to be prime in order to provide a useful hash function. If the hash table size is prime, then that's the most important thing. After all, an integer key uses, by default, a radix of 10 and it works fine.

What matters is that your radix and your table size be relatively prime, and that is, indeed, easier if the radix is prime and the table size is a different prime. To this end, we use 37 as the radix and the ascii values as the digits. This, then, is how one comes up with the popular hash function:

hash( str ) = ( str.charAt(0) + str.charAt(1) * 37 + str.charAt(2) * 37²+

... + str.charAt(N - 1)* 37^N-1 ) % P

where N = str.length(). Because this could result in a negative number (due to overflow) we bring it back into range by adding P in that case.

6A.2.4 strings Part 3: Tweaking

The only problem with this hash function is that it can take time to compute if the string is really long. There are a few modifications that help:

1. As mentioned earlier, use a different radix which admits a multiplication that can be performed by << or >> in conjunction with bitwise | and & operation.
2. Only use up to the first MAX_LEN characters, where MAX_LEN can be 3, 6, 12 or any number that gives you the desired result without costing too much in computation time.
3. Use every other letter, every third letter or every fourth letter, which is, in effect reducing your N by a factor of 2, 3, 4, etc.

Also, to keep the multiplications in range during the computation and the numbers smaller, you could mask (bitwise & or truncate) the result of each multiplication by a string of 1s, whose length is the bit length of the mask P - 1. This takes you even further afield from the radix idea and may harm the even distribution in certain cases. Some programmers do it, though.

6A.2.5 Coding a Hash Function

We have not written our hash table template class yet, but whatever it is, we'll find that the client cannot easily know what the table size is. For one thing, that size keeps changing, and unless the class provides a getTableSize() method that the client can use, the client will not know the current value. And supplying a getTableSize() method for the client to use within its hash function starts to get a little too demanding on the client. Therefore, we use the common approach: allow the client to provide a hash function which returns a large positive or negative int, prior to the %P operation. The hash table class template will then bring this into range.

In short, our class template will require and assume the existence of a hash() function that produces such an int, written by the client. With that in mind, we can show the hash functions for both int and string as outlined above.

// a hash routine for ints 
int Hash( int key )
{
    return key;
}

// a hash routine for strings that admits negative returns
int Hash( const string & key )
{
    unsigned int k, retVal = 0;

    for(k = 0; k < key.length( ); k++ )
        retVal = 37 * retVal + key[k];

    return retVal;
}

The funny thing here is that, since the only operation we require of the int hash function is the truncation by mod P, and the class template is going to do that for us, we have nothing to do. Still, we must provide the int in the form of a return in a function called Hash() because that's what a template class will need (if the underlying data type is int).

The string hash function uses a more efficient grouping of operations to compute the result, but a quick check with pencil and paper confirms this is the same thing: A + 37B + 372C + 373D = A + 37(B + 37(C + 37D)).

6A.2.6 Hash Functions For Non-Primitive Types

Every other data type you can imagine will ultimately have a key which is based on either int hashing or string hashing. Therefore, the client would write one or both of these two functions, then add another overloaded variant, which would be used by the hash table class template, namely int Hash( ObjectType ob). For example, let's say that the underlying data type is a PhoneEntry, and name is the key field. Then we would use the class's accessor getName() to extract a string from the object, then use that as input to our Hash(string). Here is the detail:

int Hash( const PhoneEntry &item )
{
   return Hash(item.getName());
}

This calls the Hash(string) function, written above. To be clear, it is only this last function that has to be named Hash() for our class template, since that template will only access it. But there is no harm in calling all of our hash functions Hash() as long as they take different argument types.

The bottom line is this: Whatever your data type, provide a function Hash() that takes that data type as an argument and returns an int. Don't worry about the table size or negative values from the client if your hash table class contains the proper range compression for you, which ours will.

6A.2.7 Template Class Use of Hash Function

Let's now look at how the template class will make use of the client-supplied Hash() function. We'll ignore all other details of the class, which will be discussed on the next page.

// ---------------------- Prototype --------------------------
template <class Object>
class FHhashSC
{
   static const int INIT_TABLE_SIZE = 97;

protected:
   int mTableSize;

public:


protected:

   int myHash(const Object & x) const;
};

// ---------------------- Definitions --------------------------
template <class Object>
int FHhashSC<Object>::myHash(const Object & x) const
{
   int hashVal;

   hashVal = Hash(x) % mTableSize;
   if(hashVal < 0)
      hashVal += mTableSize;

   return hashVal;
}

We see protected instead of private in anticipation of deriving from this class.

The function myHash() will be called by the public interface methods insert(), contains(), remove(), etc. These functions will rely on it to produce an accurate hash table index. In turn, myHash() calls a function Hash() which is neither defined nor prototyped in the class template. That's because Hash() is assumed to be prototyped and defined by the client. When the client supplies Hash(), everything works. When it doesn't, the compiler will call this fact to your attention.

An alternate approach is to tell the client to supply a Hash() that takes the table size as a parameter, and pass mTableSize into Hash().

We have just taken our first glimpse into the workings of the hash table class template: we have completed one private instance method, myHash(). Now we go on to study all the rest.