Section 3 - Threaded Binary Trees
This is a difficult section due to the programming details. It is not required for the material that comes, but it is important to at least read and know about. If you find yourself with time and interest, you can bear down on the programming details which are important if you go on to write threaded tree code.
5B.3.1 Threaded Trees and In-Order Successors
There are many improvements we can make to the theory of binary search trees and their AVL refinements. One target for acceleration is the traversal algorithm because, unlike insertion and deletion, it is O(N), not O(logN), and any fixed expenses here are going to be magnified. To start, we can try to remove recursion from the traversal process, making it a simple loop structure. This will reduce program stack overhead. This is an in-order traversal, the most common type:
void FHsearch_tree<Comparable>::traverse( FHs_treeNode<Comparable> *treeNode,
Processor func, int level) const
{
if (mRoot == NULL)
return;
if (treeNode == NULL)
return;
// we're not doing anything with level but it's there in case we want it
traverse(treeNode->lftChild, func, level + 1);
func(treeNode->data);
traverse(treeNode->rtChild, func, level + 1);
}
How can we do an in-order traversal without recursion? In-order has the same effect as visiting each node from smallest to largest. Imagine that we happened to be lucky enough to be standing on the smallest node of the tree, free of charge. We visit that node, now. Oh boy. We managed to get one node printed/processed/visited in the correct order. Now what? Well, we want its "in-order successor", that is, the node that would be visited immediately after. This would be the next highest node. There are two possibilities:
- The node has a non-null right child. In that case, I want the minimum of that subtree. That's actually something you can code directly, if you think about it: Step down to the right child, and from there, move left -- only left -- until you hit a null left child pointer. You have just found the smallest node in the right subtree of our original smallest node. That was easy! It is certainly bigger than the first node because it was in the right sub-tree. And there is nothing smaller in the right sub-tree because we found it by going left-left-left-... until we couldn't go left "no 'mo."
- The node has no right sub-tree - its right child is null. This is really easy. In this case, the in-order successor is immediately known to be the node's parent.
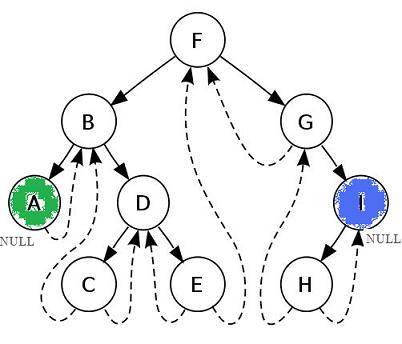In case 1, we can code a short loop to find the node's in-order successor because we are simply chasing left child links. It's a short loop. But in case 2, ironically, the "simple" case, we are at a loss. We know the successor is the parent, but how do we get to the parent? In our very early non-binary trees, we had a parent pointer, but such pointers are not common in BSTs, although they are sometimes used, as we will see. Assuming that we don't want to keep a pointer to the parent of each node, the answer to this question is the key to idea of threaded trees. Case 2 came about because there was a null in the right child field. We now change that and allow that same pointer to be used to point to the node's parent. This will allow us to step up, directly to the node's parent, its in-order successor.
If we did that for every node, we would have a single procedural way to move through the tree from smallest to largest, without recursion.
Because we are considering using the right child member, rtChild, to point to a node's parent in some nodes, and do what it was designed to -- point to the node's right child -- in other nodes, we need a signal of some sort -- a bit of data telling us how a node's right child is being used. This is the space-overhead cost of the technique: a boolean, int or char tag that tells us that either
- the rtChild member is pointing to a normal right child, or
- the rtChild member is pointing to the current node's parent (i.e., in-order successor).
If we use rtChild to point to its in-order successor we call the rtChild a "thread". That means, sometimes rtChild is a thread, and other times, it's just an ordinary right child pointer.
I have just described a threaded tree structure, specifically, a tree structure threaded for an in-order traversal. The node type for such a tree would look something like this:
template <class Comparable>
class FHthreadedNode
{
public:
FHthreadedNode( const Comparable & d = Comparable(),
FHthreadedNode *l = NULL,
FHthreadedNode *r = NULL,
bool lftThr = true,
bool rtThr = true)
:
lftChild(l), rtChild(r), data(d),
lftThread(lftThr), rtThread(rtThr)
{ }
FHthreadedNode *lftChild, *rtChild;
Comparable data;
bool lftThread, rtThread;
};
The key point is the presence of the two bools at the bottom. lftThread will be true if the lftChild is pointing to an in-order predecessor and false if it is pointing to a normal left child. Similarly, rtChild will be true if rtChild is being used as a thread, and false if it just an ordinary right child.
The biggest difference in coding with threads is the way we signal a dead-end. We don't look for NULL, but rather, a true lftThread or rtThread. A true lftThread will cause us to do whatever we did if we happened to find a null lftChild in earlier coding. As an example, let's assume that our tree was correctly threaded. We would rewrite our findMin() using the thread members (or thread bits, as they are sometimes called) like so:
template <class Comparable>
FHthreadedNode<Comparable> *FHthreadedBST<Comparable>::findMin(
FHthreadedNode<Comparable> *root) const
{
if (root == NULL)
return NULL;
while ( !(root->lftThread) )
root = root->lftChild;
return root;
}
I don't want to mislead you. findMin() could have been easily made non-recursive even without threads. But if you use threads, the above code shows how you use the lftThread bit, rather than testing for lftChild == NULL. You would never test for lftChild == NULL in a threaded tree, since it means nothing, and it rarely occurs.
This was just a taste of how the code would change if you used threads. But let's at least do the juicy part: a traversal, non-recursively. For that we'll first need a work horse function successor() that returns the in-order successor of a node. I described what this did in words in the two cases at the top of this section.
template <class Comparable>
FHthreadedNode<Comparable> *FHthreadedBST<Comparable>::successor(
FHthreadedNode<Comparable> *node)
{
if (node == NULL)
return NULL;
if (node->rtThread)
return node->rtChild;
node = node->rtChild;
while ( !(node->lftThread) )
node = node->lftChild;
return node;
}
As I stated, earlier, the simple case is covered if the parent is the in-order successor, and this is detected by a rtThread == true. Otherwise, we use a simple loop to find the in-order successor down the left side of the right sub-tree. There is a companion method predecessor():
template <class Comparable>
FHthreadedNode<Comparable> *FHthreadedBST<Comparable>::predecessor(
FHthreadedNode<Comparable> *node)
{
if (node == NULL)
return NULL;
if (node->lftThread)
return node->lftChild;
node = node->lftChild;
while ( !(node->rtThread) )
node = node->rtChild;
return node;
}
Now to solve the traversal problem. It is easily done once we have these methods in place. We don't need a public/private pair, by the way, since we are not going with recursion. So our traverse() method is a single function (in the earlier template classes, we had two versions).
template <class Comparable>
template <class Processor>
void FHthreadedBST<Comparable>::traverse( Processor func) const
{
if (mRoot == NULL)
return;
FHthreadedNode<Comparable> *node = findMin(mRoot);
do
{
func(node->data);
node = successor(node);
} while (node != NULL);
}
Notice how simple it now is, even with the elegance of recursion gone. We find the minimum, and from there, we just get the successor until we hit a NULL. (This is one of the two NULLs in every threaded tree.)
I want to be clear about threads and what they do. They do not make the insert() and remove() algorithms any easier. They are added primarily for traversals. When you have a tree that needs to be recursed quickly in O(N) time and you want very small overhead, they are useful. In fact, adding threads makes the other logic kind of messy.
5B.3.2 A Non-Lazy Deletion remove() Algorithm.
Coding a full class template for threaded trees requires, unfortunately, that we start from scratch and rewrite many of the BST algorithms. There is very little that can be reused, so inheritance is not a good option. Here is an example of a remove() method which actually keeps the recursion in place, because remove() is very hard to do without it, especially with threads. The purpose here is to see how we must maintain the threads as we do the same sort of maneuvers (which were easier before).
// very hard to remove recursion from this, so adjust pred/succ links
template <class Comparable>
bool FHthreadedBST<Comparable>::remove(
FHthreadedNode<Comparable> * &root, const Comparable &x)
{
if (root == NULL)
return false;
if (x < root->data)
if (root->lftThread)
return false;
else
return remove(root->lftChild, x);
if (root->data < x)
if (root->rtThread)
return false;
else
return remove(root->rtChild, x);
// found the node
if ( !(root->lftThread) && !(root->rtThread) )
{
// two real children
FHthreadedNode<Comparable> *minNode = findMin(root->rtChild);
root->data = minNode->data;
remove(root->rtChild, minNode->data);
}
else
{
// one or two "fake" children => at least one thread
FHthreadedNode<Comparable> *nodeToRemove = root;
// adjust nodeToRemove's in root's subtree that "thread directly up" to nodeToRemove
redirectThreadsPointingToMe(nodeToRemove);
// if a full leaf, we have to modify one of parent's thread flags and unlink
if (nodeToRemove->lftThread && nodeToRemove->rtThread)
{
adjustParentThreadFlagsAndUnlink(nodeToRemove);
// in case this was final node in tree
if (nodeToRemove->lftChild == NULL && nodeToRemove->rtChild == NULL)
mRoot = NULL;
}
else
// at least one real child, so we copy to parent
root = ( !(nodeToRemove->lftThread) )?
nodeToRemove->lftChild : nodeToRemove->rtChild;
// no completely unlinked and adjusted, so safe to remove
delete nodeToRemove;
}
return true;
}
This function really echoes the earlier BST version, but it shows two things:
- Prior to recursing, in the two early cases where we have to move left or right down the tree, we have to add an extra test, e.g., if (root->lftThread), and return false, indicating that the node was not present. We cannot simply recurse and expect the inner call to pick up the NULL. It won't because there will be no NULL.
- The final explicit case where we copy a left or right child up to the to-be-deleted node, we have a real extravaganza on our hands. Since we are cutting a node out of the tree, we have to move its successor and/or predecessor pointers and thread indicators to other nodes in its subtree.
There are two helper methods that alleviate some of the complexity of the remove() algorithm. They are invoked in the final else clause, and here are their definitions:
template <class Comparable>
void FHthreadedBST<Comparable>::redirectThreadsPointingToMe(
FHthreadedNode<Comparable> *nodeToRemove )
{
FHthreadedNode<Comparable> *minNode, *maxNode, *node;
// adjust nodes in root's subtree that "thread directly up" to root
minNode = findMin(nodeToRemove);
maxNode = findMax(nodeToRemove);
for (node = minNode; node != NULL; node = successor(node))
if (node->lftThread && node->lftChild == nodeToRemove)
{
node->lftChild = predecessor(nodeToRemove);
break; // last of only two possible threads pointing up
}
else if (node->rtThread && node->rtChild == nodeToRemove)
{
node->rtChild = successor(nodeToRemove);
}
}
// called when both flags are true, meaning one MUST be parent. find out
// which one, so we can set parent's left of right thread flag to true
template <class Comparable>
void FHthreadedBST<Comparable>::adjustParentThreadFlagsAndUnlink(
FHthreadedNode<Comparable> *nodeToRemove )
{
FHthreadedNode<Comparable> *node;
node = nodeToRemove->rtChild; // successor is parent?
if ( node != NULL )
{
if ( node->lftChild == nodeToRemove )
{
node->lftThread = true;
node->lftChild = nodeToRemove->lftChild;
}
}
// test both in case mRoot is leaf
node = nodeToRemove->lftChild; // predecessor is parent?
if ( node != NULL )
{
if ( node->rtChild == nodeToRemove )
{
node->rtThread = true;
node->rtChild = nodeToRemove->rtChild;
}
}
}
As you can see, it is messy. A lazy-deletion strategy would be somewhat easier with threaded trees, but even then you would need a hard delete, which the above code affords.
5B.3.3 Other Remarks on Threaded Trees and a Test main()
There are other challenges with threaded trees, but none that you could not overcome if you had to. One of the more insidious is that of performing a deep copy of the entire tree. This is needed for copy constructors and assignment operators. The reason this is so radically different with threaded trees is that the thread structure spreads messily across the entire tree, and is not restricted to the vicinity of each node. You just can't use the same clone() technique that we so easily wrote-up in our BST and AVL trees. The solution is to give up trying to do this in an efficient manner, and instead, accept that deep copies of threaded trees are done rarely enough that the algorithm can be a little higher level, slower, and as it turns out, actually shorter to code.
Here is a test main() and output.
// FHthreadedBST main
// CS 2C, Foothill College, Michael Loceff, creator
#include <iostream>
#include <string>
using namespace std;
#include "FHthreadedBST.h"
template <typename Object>
class PrintObject
{
public:
void operator()(Object obj)
{
cout << obj << " ";
}
};
int main()
{
int k;
FHthreadedBST<int> searchTree;
PrintObject<int> intPrinter;
searchTree.traverse(intPrinter);
cout << "initial size: " << searchTree.size() << endl;
searchTree.insert(5);
searchTree.insert(2);
searchTree.insert(20);
searchTree.insert(10);
searchTree.insert(7);
searchTree.insert(15);
cout << "new size: " << searchTree.size() << endl;
cout << "traversal: \n";
searchTree.traverse(intPrinter);
FHthreadedBST<int> searchTree2 = searchTree;
searchTree.remove(10);
cout << "\nsearchTree after removal:\n";
searchTree.traverse(intPrinter);
cout << "\n\nAttempting 100 removals: \n";
for (k = 100; k > 0; k--)
if (searchTree.remove(k))
cout << "removed " << k << endl;
cout << "\nsearchTree after deletes:\n";
searchTree.traverse(intPrinter);
cout << "\nsearchTree2 after deletes:\n";
searchTree2.traverse(intPrinter);
cout << endl;
searchTree2.insert(3);
searchTree2.insert(-5);
searchTree2.insert(38);
searchTree2.insert(40);
searchTree2.insert(21);
searchTree2.insert(21);
cout << "\nsearchTree2 after 6 insertions:\n";
searchTree2.traverse(intPrinter);
searchTree2.remove(38);
cout << "\nsearchTree2 after removal:\n";
searchTree2.traverse(intPrinter);
searchTree2.remove(5);
cout << "\nsearchTree2 after removal:\n";
searchTree2.traverse(intPrinter);
searchTree2.remove(-5);
cout << "\nsearchTree2 after removal:\n";
searchTree2.traverse(intPrinter);
searchTree2.remove(40);
cout << "\nsearchTree2 after removal:\n";
searchTree2.traverse(intPrinter);
searchTree2.remove(21);
cout << "\nsearchTree2 after removal:\n";
searchTree2.traverse(intPrinter);
cout << endl;
return 0;
}
/* ------------------ RUN -------------
initial size: 0
new size: 6
traversal:
2 5 7 10 15 20
searchTree after removal:
2 5 7 15 20
Attempting 100 removals:
removed 20
removed 15
removed 7
removed 5
removed 2
searchTree after deletes:
searchTree2 after deletes:
2 5 7 10 15 20
searchTree2 after 6 insertions:
-5 2 3 5 7 10 15 20 21 38 40
searchTree2 after removal:
-5 2 3 5 7 10 15 20 21 40
searchTree2 after removal:
-5 2 3 7 10 15 20 21 40
searchTree2 after removal:
2 3 7 10 15 20 21 40
searchTree2 after removal:
2 3 7 10 15 20 21
searchTree2 after removal:
2 3 7 10 15 20
Press any key to continue . . .
-------------------------------------------- */