Section 3 - Double Rotation

5A.3.1 Double Rotation

As I mentioned in an earlier note, the single rotations had a double left or double right structure below the center of rotation. This is an echo of the real issue: The subtree that needed to be shortened - the X subtree in the earlier diagrams, was found by starting at the central node and either going left twice or right twice.

There will be times when the node at which we are trying to "restore order" has a different problem. The subtree that is too high is found by first moving right, then immediately moving left from the central node: a zig and then a zag. Or, the symmetric condition is that the too-tall tree appears by first jogging left, then jogging right. The point is, the problem subtree is closer to the middle of the tree rather than the exterior where single rotations worked.

For example, say we insert a node by first moving left from the central node, then moving right from its child. A little zig-zag action, if you will. It turns out that the single rotation won't do the trick to rebalance the tree at that node. Therefore we now introduce the only other maneuver -- the double rotation -- that we'll need to make all of our AVL algorithms work.

Double Rotation

I will now call k₃ our the center of rotation. k₂ will always be its child and k₁ its grandchild. In double rotations, if k₂ is the left child, then k₁ will be the left->right grandchild, and likewise, if k₂ is the right child, then k₁ will be the right->left grandchild. Furthermore, I will continue to call the problem subtree -- the one that's hanging too low -- X. However, in this case, we will have two possible too-tall trees, and I'll call the second one X'. The picture will clear this up in a moment.

Again, we'll say that the AVL condition is just barely not met at k₃, specifically,

height( k3's left child ) - height( k3's right child ) = 2

In other words we assume the problem is that the left is taller than the right by 2, a little too much for the likes of AVL. The difference between this and the prior situation is that the subtree that is too tall is not found by going left twice from the center of rotation, k₃, but rather by going left, and then right. Here is a picture of the bad situation at k₃:

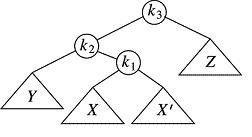
As you can see, the subtrees X and X' are not necessarily taller than Y and Z, because we have now separated out the root, k₁, which accounts for the extra height. If X (or X'), Y and Z are all, say height 9, then the diagram shows that we still have a bad AVL condition at k₃ because k₃'s right subtree, Z, has height 9 but its left subtree, rooted at k₂ has height 11 on account of either X or X' (we don't know or care which) having height 9 and nodes k₁ and k₂ adding 2 more, causing k₂ to have height 11.. The big picture here is that the problem of extra height which forms an imbalance at k₃ comes about by starting at k₃ and jogging left, then right, not left then left.

You can try to fix this by a single rotation, but you'll see it doesn't work. We will define and use a double rotation. Again, I'll deviate from the text and call this a left double rotation (the book calls it a right-left rotation). It is a double rotation, and the child of the center of rotation is the left child: we are having problems with the left of k₃ being too tall.

For all the jargon, the fix is rather simple. We start with left child, k₂ and do a single right rotation there. After that, we do a single left rotation at our central node, k₃. In other words, we do two simple single rotations in a row. That's it.

1. The first rotation will move k₁ up above k₂, but it will still be below k₃.
2. The second rotation will move k₁ up above k₃ to be the new root of the subtree.

Here's the "after" picture.

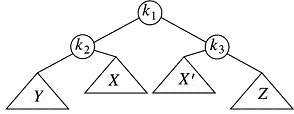
You can do the two single rotations, (a right single at k₂ followed by a left single at k₃) and you should get this picture. As you can see, balance is improved at k₃.

If the subtrees Z and k₂ were internally AVL-balanced to start out, thus making k₃ the only node where AVL was violated, then we have turned a non-AVL tree into an AVL tree.

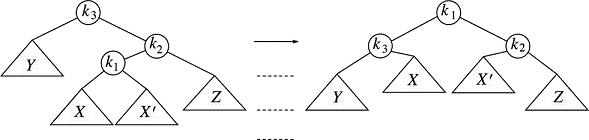
This was a left double rotation. A right double rotation helps balance a node whose right subtree is too high compared to its left because of a problem subtree, X (or X') hanging first off the right child of k₃ then off the left child of k₂. The process is similar to what we just described, with the obvious changes. Here is the picture:

5A.3.2 Double Rotation Problems

Problem 1

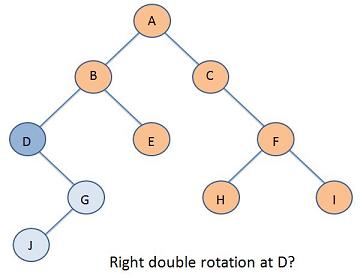
Problem 2

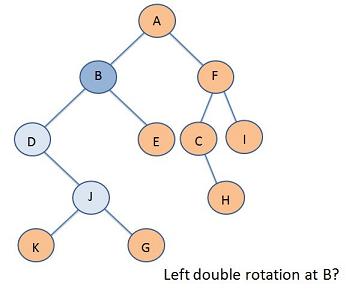
Double Rotation Answers

Problem 1

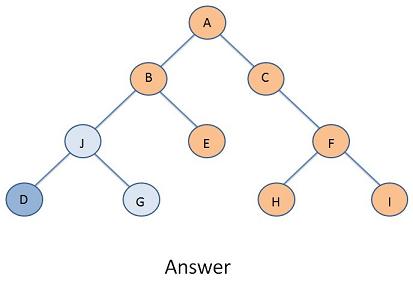
Problem 2