Section 2 - Single Rotation Practice
5A.2.1 Notes on Single Rotation
Height of a null sub-tree
When a subtree is a leaf, we say it has height 0. You already knew that, I suspect. But what about a reference that is null? There isn't even one node there, so what should we say the height of that is? You might think this is an odd question, but recall the definition of AVL-balanced. We are comparing the height of a node's left- and right-subtree. If there is either no left or no right child, one of those subtrees has no nodes at all in them. It is null "from top to bottom". So the center of rotation's left (or right) child reference is null. By definition, the null reference subtree has height -1. We would use that value when computing the difference in height between the two subtrees. For example:
Zebra
/
/
/
Tomato
Zebra's left subtree (Tomato) has height 0 and Zebra's right subtree has height -1. So Zebra is an AVL-balanced node: subtree heights differ by 1, which is fine.
Nothing to Clip
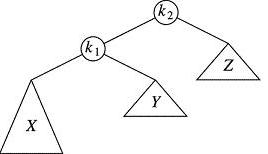
The details of the subtrees X, Y and Z were not shown. In particular, the smaller subtrees (Y and Z) might in some cases be null, and therefore have height -1. For example, in the left single rotation picture, k2 could have height 2 and Y and Z could both be empty trees, while X consists of just a single node:
Zebra (k2)
/
/
/
Tomato (k1)
/
/
/
BMW (X)
The subtrees rooted at Zebra and Tomato have only left children That's okay. This sub-tree is AVL-imblanaced at Zebra (right subtree has height -1 and left subtree has height 1, which differ by 2: bad. We can rebalance using a single left rotation centered at Zebra. You get the following:
Tomato
/\
/ \
/ \
BMW Zebra
Here, when we clip and copy the dangling "middle" child of k1 (Tomato ) after "raising it up" -- which was, Tomato's old right child -- we are really dangling nothing -- a null reference, and so there is nothing to copy over to Zebra's left child reference.
Common Properties of Single Rotation "Before" States
Finally, we notice that there is something true about all nodes on which we perform a single left or single right rotation.
- If we are performing a single left rotation, then the center of rotation (k2 in the above example) will have a left child and that child will also have a left child: we can go left twice-in-a-row from the center of rotation.
- Likewise, if we are performing a single right rotation, then the center of rotation (k2 in the above example) will have a right child and that child will also have a right child: we can go right twice-in-a-row from the center of rotation.
- More to the point, the tree, X, that is "too tall" and needs to be cranked up one notch, is somewhat on the outside of subtree in question since it is found by traveling from the central node, k2, and then either going right-right, which tends to keep X close to the right exterior of the subtree, or left-left from which tends to keep X close to the left exterior of the subtree.
It is this left-left or right-right position of the tall X that allows single rotations to work for us. We'll see that if the tall X is not so positioned, we need a different tool.
5A.2.2 Four Problems
Here are some problems to help you practice your new knowledge of single rotation. In each case I am giving you a tree which is not AVL-balanced at a particular node and asking you to do a single left (or right) rotation centered at that node. These trees are not necessarily AVL-balanced at other nodes, and the rotations I am requesting are in somewhat random places in the tree. These specific problems may not come about naturally in an actual AVL rebalancing algorithm, because it might be that one would not try to do a rotation at these exact spots before first adjusting the tree elsewhere. However, that is of no concern to us. All that matters here is that you know how to draw and erase the links at the center of rotation that I request based on the steps you just learned.
For these problems you'll need a pencil with eraser and paper. This is not about coding, it is about understanding how to do a rotation quickly and automatically. If you get a problem wrong, start over and try it again, not thinking about the answer that you saw, but re-constructing the logic on your own.
This exercise is important because without it, you have no hope of ever coding a rotation algorithm. You must first understand what you are trying to do before you hope to be able to write a program to do it.
Note: The letters are only labels for the nodes and not meant to represent any alphabetical ordering. We assume the tree is ordered before the rotations, which means they will remain ordered after. For example, looking at the main root, node A, we can surmise that key of node B < key of node A and key of node A < key of node F.
Problem 1
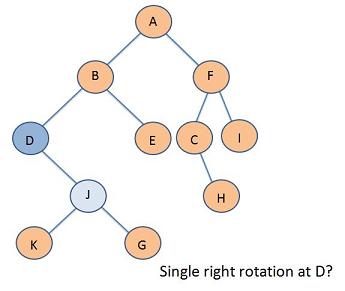
Problem 2
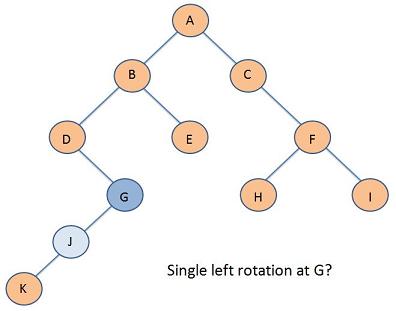
Problem 3
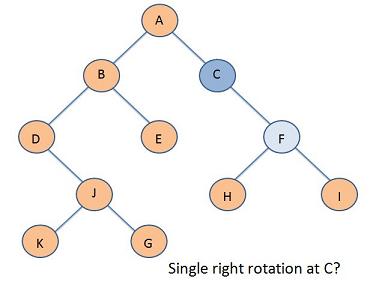
Problem 4
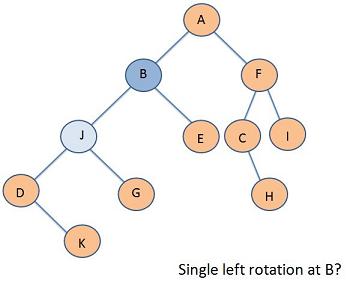
Single Rotation Answers
Problem 1
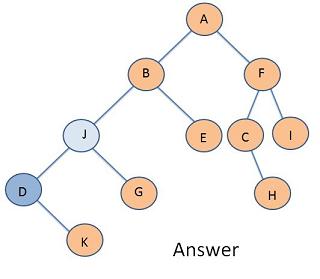
Problem 2
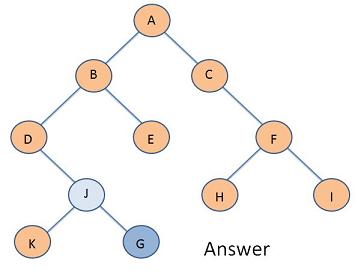
Problem 3
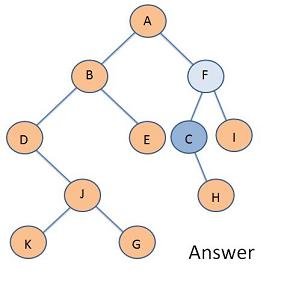
Problem 4
