Section 1 - AVL Trees

5A.1.1 Balancing Conditions and AVL Trees

While the binary search tree is a good general-purpose tree for implementing ordered data, there is no guarantee that we can get average search times of Θ(logN). A heavily imbalanced tree is only Θ(N). The factor that prevented us from getting the better estimate was the height of the tree. If the tree was imbalanced, its height was closer to N than logN.

To remedy this we add a new condition to our list of conditions that defined a BST. Before we do, let's remind ourselves, what "list of conditions" I am talking about. A BST has two conditions:

1. A Structure Condition: node has, at most, only two sub-trees.
2. An Ordering Condition: for each node, the keys in its left subtree are all < the node's key, and the keys in its right subtree are all > the node's key.

We now add a second structure condition, called the AVL balance condition after its inventors , G.M. Adelson-Velskii and E.M. Landis:

3. AVL Balance Condition: Each node's left and right subtree heights differ by at most 1.

It's important to remember that the AVL condition, like the first two conditions, must be met at every node in the tree, not just the root. If there is a violation of the AVL condition at even one node, then the tree is not AVL-balanced.

The purpose of the AVL condition is to guarantee that all operations are tightly bound by O(logN), something we could not say about general BSTs.

Here are two BSTs containing the same int keys, but only the tree on the left is AVL-balanced:

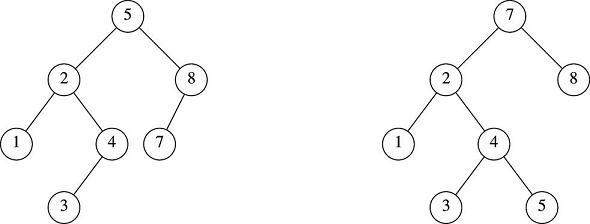
The tree on the right violates AVL at the root node (7) because its left subtree (2) has height 2, while its right subtree (8) has height 0. The tree on the left, meanwhile, has a good AVL condition at the root (5), since its left subtree (2) has height 2, and its right subtree (8) has height 1. By the way, except for the root, both trees have AVL balanced nodes, so in this case, it is only the root node on the right example that creates the problem.

This extra structure condition is called a balancing condition because it keeps the tree from becoming too lop-sided. There are other such balancing conditions, one of which is that the left and right subtrees of every node be the same height, exactly. This results in what we call a perfect binary tree. However, this is very hard to meet. In fact, I challenge anyone to find a tree that meets this condition which does not have exactly N = 2^M -1 nodes, for some integer M. Since we rarely have exactly a power of 2 minus one nodes in our database, imposing a perfect binary tree condition is not of much use. Another strong balancing condition is that a tree be complete, which means, loosely, that the only nodes missing, and keeping it from being perfect, are in the bottom level, and they are all on the right part of the bottom level. While you can get any size tree to meet such a condition, you cannot keep it ordered. So this, too, is not useful for keeping nodes sorted. It will be very important to us, though, when we study priority queues.

There are, however, alternative balancing conditions. The key thing to remember is that the AVL condition is the first easy-to-implement and very efficient balancing condition that can improve BST search times to a tight bound of O(logN).

5A.1.2 Self-Balancing Trees

So far we have been talking about adjectives, not verbs. We have a condition which a tree either meets or doesn't meet, but we need more: we need algorithms for inserting and deleting nodes in a BST that produce and preserve the AVL balance condition. When we have these algorithms, we can say that the tree is self-balancing.

Whenever you add some action to the insert and remove algorithms for any reason (such as keeping the tree balanced) you can imagine that this adds overhead. It is important, then, to keep ourselves grounded in reality. Whatever we do here to produce and maintain the AVL condition is going to add to our insert and remove times. How can we hope to make things better if this is so? The answer is that we will be adding O(1), i.e., constant time, operations to our algorithms and, in return, we will be managing the depth to be O(logN) rather than O(N). Because we found that the depth is the overriding determinant in the running time of the algorithms, this will be a great trade-off. In other words, it might take a tiny bit longer to add or remove one node to/from a tree, but we will avoid embarrassing lop-sided situations with a 100% money-back guarantee.

5A.1.3 Rebalancing By Rotation

The key move in studying AVL trees is something called a rotation. You can perform a rotation at any node in your tree, and this affects only that node's children and possibly grandchildren, nothing further down or above. The rotation has the effect of changing a few links (i.e., left- or right-child references) causing some relationship changes near the node that is the center of the rotation, and the result is always a tree which is better balanced than before.

What, exactly, is the purpose and the effect of a rotation?

• - A rotation is something we will perform after we temporarily destroy the AVL balance condition at that node by an inserting or deleting a node.
• - A rotation will become part of the AVL insertion or deletion algorithm of an AVL tree. It will add extra leg work for the tree designer, but the client will not even know about it.
• - A rotation will preserve the ordering condition required of all binary search trees: the tree was ordered before the rotation and will not alter that fact.
• - For a rotation to be effective, we have to do it at the right time, in the right place and, if more than one rotation is required, in the correct order.

Since rotations are modular components that can be used by both insertion and deletion algorithms, we can study them first in isolation They are quite short, and for those who understand them, extremely simple. However, getting comfortable with them requires each student to construct his or her own mental image of what's going on. They seem strange at first.

The web is full of different programmers' attempts at explaining rotations. It seems like everyone who uses them thinks he has the perfect way to express these mysterious maneuvers, but the more versions you read, the more confused you can get. You just have to buckle down and study the algorithm until you finally "see" it. Here is one man's version of how rotations work.

There are two types of rotations, a single rotation and a double rotation. On this page, I want you to just focus on the single rotation.

Single Rotation

We always pick one node to be the center of rotation. The assumption is that, at that node (which I will call k₂) the AVL balance condition is not met. I'll repeat the AVL balance condition here for reference:

3. AVL Balance Condition: Each node's left and right subtree heights differ by at most 1.

Let's say that the AVL condition is just barely not met at k₂, specifically,

height( k₂'s left child ) - height( k₂'s right child ) = 2

In other words we assume the problem is that the left is taller than the right by 2, a little too much for the likes of AVL. Here is a picture of the bad situation at k₂:

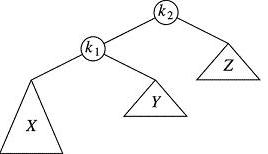
The triangles represent subtrees which might have thousands of nodes, and their sizes reflects their heights. From the picture we see that subtrees Y and Z have the same height and subtree X is "taller" than those two. Also, we've put some extra information into k₂'s left sub-tree, which I will now explain.

Pretend that the height of subtree X is 10, and both Y and Z have height 9. So k₁'s left subtree, X (height, 10) is slightly higher than its right subtree, Y (height 9), but only by 1 - within the AVL limits. In other words, k₁ does not violate AVL. Meanwhile, one floor up, k₂'s right subtree, Z (height 9) is shorter than its left subtree k₁(height 11) by 2. This does violate AVL. (Do you see why k₁ has height 11? Its larger subtree, X, is 10, and k₁ is one above it. Stating that solely in terms of k₂, we would say that k₂'s left subtree has height 11 and its right subtree has height 9.)

Summarizing our predicament, k₂'s left subtree, while slightly imbalanced, is at least within AVL limits, and thus okay. But k₂, itself, has problems because its left subtree has height 11 while its right has height 9. They differ by 2 and we want to reduce that. Understanding the problem is half the battle.

Now for the solution. Imagine that the straight lines connecting each node to its children/subtrees are strings, and the nodes k₁and k₂ are disks - hockey pucks or yo-yos. Look again, at the picture above. Now, raise yo-yo k₁ up a bit so it is above k₂. k₁ will then have three strings dangling from it:

1. the string on the far left of k₁ will hold subtree X as its left child.
2. the string on the far right of k₁ will hold node k₂.
3. the string in the middle of k₂ will hold subtree Y, swinging in the middle, illegally.

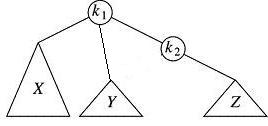
We fix that by clipping Y from k₁ and re-attaching it to the left of k₂, as k₂'s new left child. Here's the picture after you do that:

If you can connect my words with the diagrams, you have just experienced your first single rotation. More specifically, we have rotated k₂ with its left sub child, k₁. This is also called a single left rotation at k₂(or left single rotation -- please allow for either modifier to come first in the discussion).

The picture suggests that we have improved the AVL-balance, but have we? Let's count. X, unchanged, has height 10, so k₁ (the new root) has a left subtree of height 10. Meanwhile, both Y and Z were -- and still are -- height 9, but they are now both below k₂, equally, making k₂'s height 9 + 1 = 10. Therefore, the new tree is AVL-balanced at the root, k₁. Now, both k₁ and k₂ satisfy the AVL balance condition. We have not touched anything inside X, Y or Z, so they are exactly as before. We have improved the AVL condition at one node, and preserved the ordering and structure of everything else. Our single rotation, under the seemingly specialized conditions I laid out for you, has, indeed, improved the situation.

By the way, if subtrees X, Y and Z, were internally AVL-balanced to start out, thus making k₂ the only node where AVL was violated, then what have we done? We have turned a non-AVL tree into an AVL tree. This is an important thing to realize.

All that comes next are just simpler variations of, and based upon, what we did above, so I suggest that you read this last section again now, and then review it over the next few days, so that you really have the picture in your mind. It will serve you well when you are reading or writing AVL rotation code.

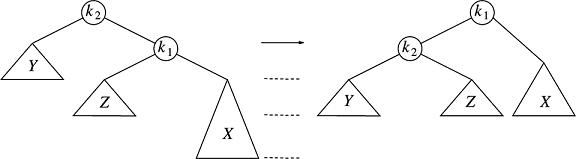
Once again, I'm calling the subtree, X, the largest of the three subtrees by enough to make the tree imbalanced at k₂. It will often be true, but not always, that the Y and Z will be the same height, and X will be exactly one taller, causing a unique AVL imbalance at k₂.

Please note that I am using a slightly different naming convention than the textbook. In all my examples, k₂is the center of rotation and k₁ is its child before the rotation. After the rotation, k₁ will be raised up and k₂ lowered. The textbook always keeps k₁ to the left of k₂ as though the subscripts 1 and 2 represent the key values.

Also, I am always using X as the symbol for the tallest (highest) subtree in the examples. Sometimes it appears on the left, other times on the right. The text uses X as the left-most subtree, regardless of its height, suggesting that the X is alphabetically or order-wise, left of Y and Z. In my diagrams X can appear to the left or right of Y and/or Z -- all that matters is that I am calling X the tallest subtree and one that needs to be brought closer to the central node to improve balance.

Since ordering will be naturally preserved in all these operations, I don't think it pays to indicate the ordering in the labels. It is more important to understand what the depth of each subtree is, and which nodes are the center of rotation.