Section 1 - Binary Trees

4B.1.1 Binary Trees as Algorithm Support

We've seen how general trees can be used to store data that is intrinsically tree-like, but one of the universally used trees has nothing to do with the structure of the data. Rather it is chosen for the way in which the data it contains is to be accessed. For large data sets, this gives a very fast running time. I'm talking about the binary search tree.

A binary tree is a tree in which the nodes have, at most, two children, traditionally called the left child and the right child. This restriction makes it much easier to lash-up an implementation for this data structure since we don't have the hassle of not knowing how many siblings or children nodes have. So we expect this to be a little more well-behaved data structure, and, indeed, it is. With that, we can present the basic node structure, which I'll call FHs_treeNode:

// ---------------------- FHs_treeNode Prototype --------------------------
template <class Comparable>
class FHs_treeNode
{
public:
   FHs_treeNode( const Comparable & d = Comparable(), 
      FHs_treeNode *lt = NULL, 
      FHs_treeNode *rt = NULL)
      : lftChild(lt), rtChild(rt), data(d)
   { }

   FHs_treeNode *lftChild, *rtChild;
   Comparable data;
};

It's pretty simple: two pointers and the data. Also the only method is a constructor. Don't be alarmed by the public status of the data. These objects will be fully protected by their being private members of the tree class in which they are used. While a client might be able to instantiate their own nodes, they can never touch those that will be part of our larger tree structure.

4B.1.2 Binary Search Trees

The binary nature of binary trees provides what we call a structure condition on the tree. The structure of such trees is restricted by the limitation of no more than two children per node. Some applications place no more restrictions than this on the data structure. One such is the storage and evaluation of numerical expressions like:

(a + (b * c)) + (((d * e) + f) * g)

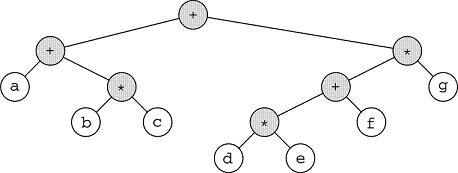
We won't study expression trees in our module here, but you can read about them in the textbook.

Instead, we want to impose a second restriction on our trees, called an ordering condition, which requires that, very loosely stated, the data stored in every node's left child be less than the data in the node's right child. As a matter of fact, we want a stronger condition:

Ordering Condition

The data in the left subtree of any parent node are less than the parent data, and the data in the right subtree are greater than the parent data.

Any tree that has this additional property is called a binary search tree, or sometimes just a search tree or BST. Here is a binary search tree that has int data:

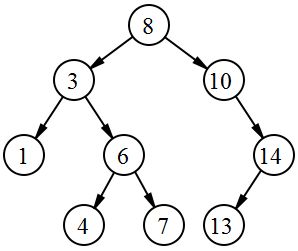
This ordering condition has an implied requirement about the data stored in the data field, namely that it have a < operator (or less-than ordering) intrinsic to the data. This is satisfied with most primitive types (ints ,chars, doubles) and even strings, and can also be designed into our user-defined classes. In fact, I have already indicated how I did this with my iTunesEntry class, where a client programmer can switch between three different search key members on which to order a collection of iTunesEntry objects. Because of this implicit requirement, when writing the template class, FHsearchTree, I have replaced the type parameter name Object with the parameter name Comparable. This helps remind us that we expect (in fact demand) that class Comparable overload < relation in a reasonable way.

4B.1.3 The FHsearch_tree Class Overview

The operations typical of a binary search tree are somewhat simpler to state than those general trees. In particular, we never allow the client to see, touch or know about the tree nodes. The client can only insert data into the tree and remove data from it. Here are some of the public methods we'll want our BST to have.

template <class Comparable>
class FHsearch_tree
{
protected:
   int mSize;
   FHs_treeNode<Comparable> *mRoot;

public:
   FHsearch_tree() { mSize = 0; mRoot = NULL; }
   ~FHsearch_tree() { clear(); }

   const Comparable &findMin() const;
   const Comparable &findMax() const;

   bool insert(const Comparable &x);
   bool remove(const Comparable &x);

   template 
   void traverse(Processor func) const { traverse(mRoot, func); }
   
   // several pubic and private methods not shown
};

We use the protected storage class for data in anticipation of subclassing from the FHsearch_tree class. This will be very handy when we study search tree derivatives such as the AVL tree. The data, constructor and destructor speak for themselves. findMin() is the public half of a pair of methods, the likes of which we have seen more than once. It will call an almost identical findMin( FHs_treeNode<Comparable> *root) that takes over by recursing until it finds what it is looking for and returns to the public findMin(). Let's look at the two method definitions. First the public version.

The public findMin():

template <class Comparable>
const Comparable & FHsearch_tree<Comparable>::findMin() const
{
   if (mRoot == NULL)
      throw EmptyTreeException();
   return findMin(mRoot)->data;
}

This findMin() throws an exception in case of an empty tree. This is the only chance for error, since if there is even one node in the tree, we must have a minimum. If the tree is not empty, it calls the private findMin() which will return the node (not the data) that contains the minimum of the tree. The function then "unwraps" the found minimum node to expose the data within it, which is then returned to the client.

Next we inspect the private findMin() which is the work horse function that recurses down the tree, looking for the minimum. The logic is straightforward, and cleaner than the recursive logic we have seen in the general tree. This typifies the ease with which BST algorithms work. Since we are finding the minimum, we simply follow the left children all the way down the tree until we hit a NULL. .

The private findMin():

template <class Comparable>
FHs_treeNode<Comparable> *FHsearch_tree<Comparable>::findMin(
   FHs_treeNode<Comparable> *root) const
{
   if (root == NULL)
      return NULL;
   if (root->lftChild == NULL)
      return root;
   return findMin(root->lftChild);
}

findMax() is nearly identical to findMin() and I'll let you either anticipate it yourself based on what we just did, or look at the include file.

We are going to see this public/private pairing repeatedly, and you should study it for full comprehension. You should be getting used to it by now.

4B.1.4 insert() and remove()

These next two functions form a useful pair. Each public version calls its private alter-ego, so let's look at both public functions first.

The public insert() and remove():

These are nearly identical to one another. They test the success or failure of their private, recursive, counterparts and if there was a success, they increment or decrement the mSize.

template <class Comparable>
bool FHsearch_tree<Comparable>::insert(const Comparable &x)
{
   if (insert(mRoot, x))
   {
      mSize++;
      return true;
   }
   return false;
}

template <class Comparable>
bool FHsearch_tree<Comparable>::remove(const Comparable &x)
{
   if (remove(mRoot, x))
   {
      mSize--;
      return true;
   }
   return false;
}

All the work is done in the private, recursive, versions so we turn to them now.

The private insert():

Note

In what follows, I will usually use the term private for unexposed methods. However, in practice, some or all of these methods will be protected. This costs nothing, and allows us to derive classes from FHsearch_tree which can access these methods and data, which are off-limits to all clients.

The private insert()'s job is to look within the subtree rooted at root, and search for x. It does this by moving down the tree, going left if x < root->data and going right if x > root->data.

If root is NULL, we take that to mean we have found the place to put x, so we build a node around it and hang it in the tree. If this is not clear in your mind, then you need to draw a picture, using the kind of data in the pictures at the top of this page, and play computer until you understand it. It should become second nature to you very quickly. In the following code, we have to test for NULL first, because we cannot recurse if root is NULL.

template <class Comparable>
bool FHsearch_tree<Comparable>::insert(
   FHs_treeNode<Comparable> * &root, const Comparable &x)
{
   if (root == NULL)
   {
      root = new FHs_treeNode<Comparable>(x, NULL, NULL);
      return true;
   }
   else if (x < root->data)
      return insert(root->lftChild, x);
   else if (root->data < x)
      return insert(root->rtChild, x);

   return false; // duplicate
}

One thing you see a lot in this class is the use of reference parameters for node pointers. A formal parameter of the form

some_func( ...,  Node * & p, ... )

This is just like any other reference parameter -- it means p is passed by reference. If we modify p in the function, then the caller's version gets modified. It just so happens p is a Node*, which means we can alter the pointer of the client, but that is nothing special. Node*, int, string -- they are all just data types and obey the same basic parameter passing rules. The use of & means what it always meant, but it looks a little funny right next to a *. Now that I've explained it, this humor should disappear. We need to pass the pointer root by reference in this method so that the terminal case of the recursion (i.e., we found a NULL) can set the child pointer of the calling object, one recursive level up, to point to the new node we are creating.

The private remove():

The remove() method is a little longer, because we not only have to find something, but make changes once we do. In the case of insert(), we were always at a leaf when the action happened, but remove() can find action very high up in the tree, requiring us to restring some node pointers.

We search for x in the tree, moving left or right as needed until we find the node containing it. That part is easy. If x is neither less than nor greater than root->data, we must be directly on top of the node we want to remove -- we have found it. That's where we get to the comment // found the node.

template <class Comparable>
bool FHsearch_tree<Comparable>::remove(
   FHs_treeNode<Comparable> * &root, const Comparable &x)
{
   if (root == NULL)
      return false;

   if (x < root->data)
      return remove(root->lftChild, x);
   if (root->data < x)
      return remove(root->rtChild, x);

   // found the node
   if (root->lftChild != NULL && root->rtChild !=NULL)
   {
      FHs_treeNode<Comparable> *minNode = findMin(root->rtChild);
      root->data = minNode->data;
      remove(root->rtChild, minNode->data);
   }
   else
   {
      FHs_treeNode<Comparable> *nodeToRemove = root;
      root = (root->lftChild != NULL)? root->lftChild : root->rtChild;
      delete nodeToRemove;
   }
   return true;
}

At the point where we reach the // found the node comment we have two cases:

Case 1: The node contains both a left and right child. In this case we search for the minimum of the right subtree and copy that data into the node we are removing. After the copy, we actually are reusing that node - we have just removed the data, not the node. But now we have that old minimum node in the right subtree which is no longer needed, so we remove that, recursively. This one top-level removal might cause a cascade of a few removals as we move minima up the tree.

Case 2: The node is missing either a left or right child. Whichever child it is not missing, copy that entire child node up to the node we want to delete. This effectively pulls one of its subtrees up one level, squeezing out the node to be removed. (If you are worried about both children being NULL, don't. Nothing special or bad happens there.)

The logic is there, and the narrative can be studied as you attempt to follow the code.

4B.1.5 traverse()

Traversals of BSTs are almost always an in-order traversals. We implement ours by taking the idea of our earlier FHtree::traverse(), but making use of the simpler form afforded by binary trees. The public member of this pair was already shown in-line. Now we look at the private member, whose implementation is recursive. As I did with the FHtree::traverse(), I will show you the code as if it were defined in-line, but in the include file I have it prototyped and defined externally.

template <class Processor>
void traverse( FHs_treeNode<Comparable> *treeNode, Processor func) const
{
   FHs_treeNode<Comparable> *child;

   if (treeNode == NULL)
      return;

   traverse(treeNode->lftChild, func);
   func(treeNode->data);
   traverse(treeNode->rtChild, func);
}