Section 2 - Analysis of Recursive Tree Methods

4A.2.1 FHtree::find()

The definition of the remaining find() method is a great study for tree recursion. Here is the prototype, again:

FHtreeNode<Object> *find(
   FHtreeNode<Object>  *root, const Object &x, int level = 0);

It takes the original parameter, Object &x, which of course is the main reason for the method - we are trying to "find" x in this tree somewhere. Then, because it is our second, overloaded variant, intended for recursive calls, it has to have an extra parameter which helps each recursive call reach its terminal case. This is the root parameter, an FHtreeNode* that represents the root, under which, we will search. Thus, we will only look for x in the root subtree. If we were looking for a J and passed in a root that pointed to E, we would have a successful find (see the diagram for reference):

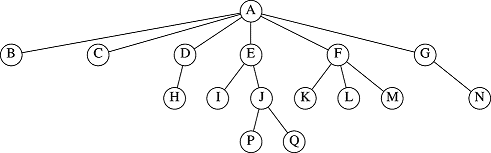
However, if we searched for J in a function call that passed in a pointer to D or F, we should not find the object -- the return should be NULL. Here is the full definition of find():

template <class Object>
FHtreeNode<Object>* FHtree<Object>::find(FHtreeNode<Object> *root, 
   const Object &x, int level)
{
   FHtreeNode<Object> *retval;
 
   if (mSize == 0 || root == NULL)
      return NULL;

   if (root->data == x)
      return root;

   // otherwise, recurse.  don't process sibs if this is the original call
   if ( level > 0 && (retval = find(root->sib, x, level)))
      return retval;
   return find(root->firstChild, x, ++level);
}

Take it slow and it should make sense. The first if statement disposes of the case where the main tree is empty or the recursive subtree in which we are searching is empty. The latter happens if we have looked all the way down to some leaf and still have not found our x. This results in the NULL return. Always remember that we don't know how many levels down we are when we return this NULL, and it may not be the last word. You have to take a "that's not my problem" attitude when working with recursion. Always focus only on your current level, and if you do that right, the function will work.

The second if statement handles the "found" case. This is the easiest one to understand.

So we have our "escape" case, always necessary in recursion. If we find our object or if we get to a NULL, we return without recursion (and eventually one of these things will happen).

But what happens if those cases are not caught? Control passes to the third if statement which makes a recursive call. This is a little tricky, but we can get it:

   // otherwise, recurse.  don't process sibs if this was the original call
   if ( level > 0 && (retval = find(root->sib, x, level)))
      return retval;

We are recursing to the sibling on the right. In order to do a search we need to thoroughly look inside the entire subtree, and this means the children and siblings. So this call represents the test on all siblings. But note that we only search the siblings if level > 0. That's because if this were the original call (i.e., from the top level) we would not want to test the sibling subtree since it is not part of the root subtree in that case. For example, say we are looking for node L in the subtree E. From the diagram you know that there is no L in the E subtree. So we should get a NULL back. But if we processed Node E's siblings, this recursive step (without the level > 0 test) would search E's next sibling, namely F and there it would eventually find L. That would be a mistake. How do we avoid it? The simple thing to do is not search E's sibling! But, that doesn't mean we never want to recurse on siblings, so we can't just omit this if statement. Again, suppose the client was searching the E subtree, but this time for node P. Here is the tree for reference, with the physical pointers:

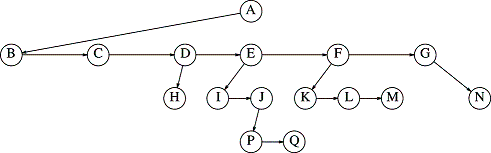
This time, when we get to E's child I we do want to test everything in that level, including I's next sib, J. How do we distinguish these two cases? This is where the int level comes into play. In the original call, we set level = 0, indicating that we were at the top of the client's search subtree. In that call, we didn't look at siblings. However, in further recursive calls, we will ++level, boosting to it 1 (and greater). In any call which has a level > 0, we are below the original root, and therefore must check the siblings. That's a lot of explanation for this recursive test. If we find what we are looking for, we are done: you can only return one found node pointer. If we don't find it, though, we go on to the children of root, as you can see in the last recursive call.

From a recursive standpoint, it is critical that we are always passing a new root that gets us closer to the leaf by calling a physically smaller tree each time. Indeed, in either the sibling or child recursive call, the root we are passing is a subtree that does contain fewer nodes than we came in with.

Time for a pause. You have to understand every molecule of this method before you can go on. It contains the essence of all tree algorithms. So study, experiment and when you have a specific question, ask. Nothing that comes after will make sense until you have digested this one function. You need to be able to write functions like find() in your sleep when you are building and processing trees.

4A.2.2 More find()s!

This last analysis covered two member functions. Actually there are also two const versions which we must provide in case the client is using const FHtrees and const FHtreeNode*s. This gives a total of four versions of find(). Here are all four prototypes. The two new method definitions are almost identical to the ones we presented and can be found in the include file.

   FHtreeNode<Object> *find(const Object &x) { return find(mRoot, x); }
   FHtreeNode<Object> *find(FHtreeNode<Object> *root, 
      const Object &x, int level = 0);
   const FHtreeNode<Object> *find(const Object &x) const { return find(mRoot, x); }
   const FHtreeNode<Object> *find(const FHtreeNode<Object> *root, 
      const Object &x, int level = 0) const;

4A.2.3 addChild()

We can't really do any of this without a method to build trees. Our addChild() method does this for us.

FHtreeNode Constructors

In addChild(), we instantiate a new FHtreeNode which means calling that class's constructor. I did not show those constructors in the last page, so I'll do that now. There are two - a public for clients, and a protected or private, just for friends like FHtree. The only difference is that the protected version allows the setting of the myRoot pointer which "bookkeeps" the compatibility of FHtreeNodes with FHtrees. This is a tricky statement that doesn't quite have to make complete sense yet. It will when you see the implementation in the next few method definitions.

template <class Object>
class FHtreeNode
{
   // members not shown ...

public:
   FHtreeNode( const Object & d = Object(), 
      FHtreeNode *sb = NULL, FHtreeNode *chld = NULL, FHtreeNode *prv = NULL )
      : firstChild(chld), sib(sb), prev(prv), data(d), myRoot(NULL)
   { }
private:
   // for use only by FHtree
   FHtreeNode( const Object & d, 
      FHtreeNode *sb, FHtreeNode *chld, FHtreeNode *prv,
      const FHtreeNode *root )
      :  firstChild(chld), sib(sb), prev(prv), data(d), myRoot(root)
   { }
};

addChild()

If we start with an empty tree, we will add a node like so, using NULL as our parent:

int main()
{
   FHtree<string> sceneTree;
   FHtreeNode<string> *tn;

   // create a scene in a room
   tn = sceneTree.addChild(NULL, "room");

The addChild() function should return a pointer to the newly created FHtreeNode so we can use that if we want to add children to that node. We capture the return node pointer so that we can then use it to do that:

   // add three objects to the scene tree
   sceneTree.addChild(tn, "Lily the canine");
   sceneTree.addChild(tn, "Miguel the human");
   sceneTree.addChild(tn, "table");

With that introduction to addChild(), we can write it.

The first part will handle the cases where

we have a legal empty tree and our client knows it, adding the first root node to the tree, and
we have some illegal calls because of incompatible objects.

This covers the first three if statements in the method definition below.

template <class Object>
FHtreeNode<Object>  *FHtree<Object>::addChild( 
   FHtreeNode<Object>  *treeNode, const Object &x )
{
   // empty tree? - create a root node if user passes in NULL
   if (mSize == 0)
   {
      if (treeNode != NULL)
         return NULL; // silent error: something's fishy.
      mRoot = new FHtreeNode<Object>(x, NULL, NULL, NULL);
      mRoot->myRoot = mRoot;
      mSize = 1;
      return mRoot;
   }
   if (treeNode == NULL)
      return NULL; // silent error inserting into a non_null tree with a null parent
   if (treeNode->myRoot != mRoot)
      return NULL;  // silent error, node does not belong to this tree

   // push this node into the head of the sibling list; adjust prev pointers
   FHtreeNode<Object>  *newNode = new FHtreeNode<Object>(x, 
      treeNode->firstChild, NULL, treeNode, mRoot);  // sib, child, prev, root
   treeNode->firstChild = newNode;
   if (newNode->sib != NULL)
      newNode->sib->prev = newNode;
   ++mSize;
   return newNode;
}

tree pic If we get past those if statements, we have a non-NULL and compatible treeNode pointer representing the new parent. The next few lines construct a new FHtreeNode in which to store x, and then link up the node to the parent. I will not expostulate on the details, partly because they are not crucial, and partly because you can always study the code on your own. I will say that we are "pushing" the new node onto the front of the sibling list, rather than tacking it on to the rear. This tells us that we have to change two links outside our newly constructed node:

the parent's firstChild pointer (to point to this new node)
the previous (*firstChild) object of this parent so that its prev pointer (which used to point to its parent) now points to the new node.

To summarize, the instantiation of the newNode(x, ...) places x in a new node that gets its own internal links passed to the constructor. That's followed by two adjustments to the external nodes' pointers.

4A.2.4 remove()

There are three overloaded remove() methods. I'll show you one and give a short description. This is the version that takes an FHtreeNode* object to be removed. There are others that take Object &x objects.

After studying find() you should be able to follow the logic here without too much trouble. The summary is:

We check for errors and return silently if we find them.
We remove all the children, recursively in a while loop.
We prepare to remove our current nodeToDelete by adjusting the pointers of its parent or left sibling, whichever applies (there must be exactly one of those).
We also adjust any possible right sibling's prev pointer to point around our to-be-deleted node.
We delete the node.
We decrement the mSize count.

template <class Object>
void FHtree<Object>::removeNode(FHtreeNode<Object> *nodeToDelete)
{
   if (nodeToDelete == NULL || mRoot == NULL)
      return;
   if (nodeToDelete->myRoot != mRoot)
      return;  // silent error, node does not belong to this tree

   // remove all the children of this node
   while (nodeToDelete->firstChild)
      removeNode(nodeToDelete->firstChild);

   if (nodeToDelete->prev == NULL)
      mRoot = NULL;  // last node in tree
   else if (nodeToDelete->prev->sib == nodeToDelete)
      nodeToDelete->prev->sib = nodeToDelete->sib; // adjust left sibling
   else
      nodeToDelete->prev->firstChild = nodeToDelete->sib;  // adjust parent

   // adjust the successor sub's prev pointer
   if (nodeToDelete->sib != NULL)
      nodeToDelete->sib->prev = nodeToDelete->prev;

   delete nodeToDelete;
  --mSize;
}

4A.2.5 Complete FHtree Prototype

There are other methods in the FHtree interface and I'll present them below. After including (and studying) this include file, you can use it in a client, which I show in the next section.

FHtree Prototype

template <class Object>
class FHtree
{
private:
   int mSize;
   FHtreeNode<Object> *mRoot;

public:
   FHtree() { mSize = 0; mRoot = NULL; }
   FHtree(const FHtree &rhs) { mRoot = NULL; mSize = 0; *this = rhs; }
   ~FHtree() { clear(); }
   bool empty() const { return (mSize == 0); }
   int size() const { return mSize; }
   void clear() { removeNode(mRoot); }
   const FHtree & operator=(const FHtree &rhs);

   FHtreeNode<Object> *addChild( FHtreeNode<Object> *treeNode, const Object &x );

   FHtreeNode<Object> *find(const Object &x) { return find(mRoot, x); }
   FHtreeNode<Object> *find(FHtreeNode<Object> *root, 
      const Object &x, int level = 0);
   const FHtreeNode<Object> *find(const Object &x) const { return find(mRoot, x); }
   const FHtreeNode<Object> *find(const FHtreeNode<Object> *root, 
      const Object &x, int level = 0) const;

   bool remove(const Object &x) { return remove(mRoot, x); }
   bool remove(FHtreeNode<Object> *root, const Object &x);
   void removeNode(FHtreeNode<Object> *nodeToDelete);   

   void display(FHtreeNode<Object> *treeNode = NULL, int level = 0) const;

   template 
   void traverse(Processor func, FHtreeNode<Object> *treeNode = NULL) const;

private:
   FHtreeNode<Object> *clone( FHtreeNode<Object> *root) const;
   void setMyRoots(FHtreeNode<Object> *treeNode);
};

4A.2.6 Complete Client Listing

Here is a client that demonstrates the creation and display of a tree. This symbolizes a tree data structure used in a computer animation program. In each subtree, there would be other information, most notably a 4x4 motion matrix (representing the mathematical rotations, scaling and translation of the sub-assembly in what are called "homogeneous coordinates") . We don't include that here, as it is superfluous to the understanding of the data structure. We are displaying the tree hierarchical structure textually by indenting each level an extra space.

// FHtree main
// CS 2B/C, Foothill College, Michael Loceff, creator

#include <iostream>
#include <string>
using namespace std;

#include "FHtree.h"

int main()
{
   FHtree<string> sceneTree;
   FHtreeNode<string> *tn;

   // create a scene in a room
   tn = sceneTree.addChild(NULL, "room");

   // add three objects to the scene tree
   sceneTree.addChild(tn, "Lily the canine");
   sceneTree.addChild(tn, "Miguel the human");
   sceneTree.addChild(tn, "table");

   // add some parts to Miguel
   tn = sceneTree.find("Miguel the human");

   // Miguel's left arm
   tn = sceneTree.addChild(tn, "torso");
   tn = sceneTree.addChild(tn, "left arm");
   tn =  sceneTree.addChild(tn, "left hand");
   sceneTree.addChild(tn, "thumb");
   sceneTree.addChild(tn, "index finger");
   sceneTree.addChild(tn, "middle finger");
   sceneTree.addChild(tn, "ring finger");
   sceneTree.addChild(tn, "pinky");

   // Miguel's right arm
   tn = sceneTree.find("Miguel the human");
   tn = sceneTree.find(tn, "torso");
   tn = sceneTree.addChild(tn, "right arm");
   tn =  sceneTree.addChild(tn, "right hand");
   sceneTree.addChild(tn, "thumb");
   sceneTree.addChild(tn, "index finger");
   sceneTree.addChild(tn, "middle finger");
   sceneTree.addChild(tn, "ring finger");
   sceneTree.addChild(tn, "pinky");

   // add some parts to Lily
   tn = sceneTree.find("Lily the canine");
   tn = sceneTree.addChild(tn, "torso");
   sceneTree.addChild(tn, "right front paw");
   sceneTree.addChild(tn, "left front paw");
   sceneTree.addChild(tn, "right rear paw");
   sceneTree.addChild(tn, "left rear paw");
   sceneTree.addChild(tn, "spare mutant paw");
   sceneTree.addChild(tn, "wagging tail");

   // add some parts to table
   tn = sceneTree.find("table");
   sceneTree.addChild(tn, "north east leg");
   sceneTree.addChild(tn, "north west leg");
   sceneTree.addChild(tn, "south east leg");
   sceneTree.addChild(tn, "south west leg");

   sceneTree.display();

   sceneTree.remove("spare mutant paw");
   sceneTree.remove("Miguel the human");
   sceneTree.remove("an imagined higgs boson");

   sceneTree.display();

   return 0;
}

/* ------------------ RUN -------------
room
 table
  south west leg
  south east leg
  north west leg
  north east leg
 Miguel the human
  torso
   right arm
    right hand
     pinky
     ring finger
     middle finger
     index finger
     thumb
   left arm
    left hand
     pinky
     ring finger
     middle finger
     index finger
     thumb
 Lily the canine
  torso
   wagging tail
   spare mutant paw
   left rear paw
   right rear paw
   left front paw
   right front paw
room
 table
  south west leg
  south east leg
  north west leg
  north east leg
 Lily the canine
  torso
   wagging tail
   left rear paw
   right rear paw
   left front paw
   right front paw
Press any key to continue . . .
-------------------------------------------- */