Section 1 - General Trees

4A.1.1 The Language of Trees

A tree is a data structure containing nodes that are organized by a parent-child-sibling relationship. There is always a root node that is at the highest level of the tree (which makes it more of an upside-down tree), and below the root are one or more direct children, each pictorially attached to the root with a line. Each of these children can be the parent of further children and so on until you come to some nodes that have no children. These are referred to as leafs or leaf nodes. Here is a picture from a textbook by Nyhoff that summarizes the general structure of a tree.

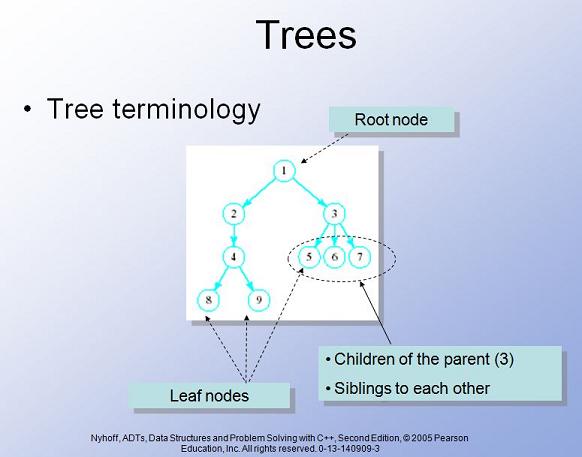
Every node is the root of a subtree. For example, node 2 is the root of the subtree consisting of it and everything below it (which is the left side of the main tree in the above picture). Node 3 is the root of a small subtree consisting of it and its three children, nodes 5, 6 and 7.

Depth refers to how many levels below the root a node is. A root node, like node 1 is said to be at depth zero and nodes 8 and 9 would be at depth three.

The height of any node would be how many levels, "worst case", there are below that node (going towards the deepest node). So the height of node 2 is two, the height of node 1 is three, and the height of node 6 is zero.

If we are discussing the depth of a node in a subtree, we consider its position only in that subtree, and not the larger tree. So, in the subtree whose root is node 4, node 4 has depth zero and node 9 has depth one. Therefore, we see that depth is not an absolute, but can change depending on which subtree we are talking about.

Height, on the other hand, is independent of the subtree we are considering, because height is measured downward, not upward.

4A.1.2 Example Applications

Examples of tree data structures are:

1. The directory/folder structure of any operating system like unix, Mac or Windows.
2. A taxonomic organization of plants or animals by their official names (kingdom, phylum, class ... genus, species).
3. Temporary structures built by your compiler that represent numerical expressions like "(2*x + exp(s - .5) * ( (s + 3)/(s - 2) + sin(x))".
4. An object in a computer animation, such as a zebra or a person. Each movable assembly, like an arm, is the root of a subtree whose children all move together with the root. For example, an arm would have an elbow and forearm as its children. The forearm would have the hand as its child. The hand would have the five fingers as its five children. Each finger would have a single child for the bone section below it. When computing motion of the object in the tree, we would move an entire subtree by moving its root, all the other items going along for the ride. If, in addition to the arm movement, the thumb also moves, we have to combine the two movements to determine the resultant position of the thumb. Computer animation and real-time simulation programmers deal with this in great detail.
5. Linguistic phrase structure of a sentence can be organized like a tree, with each phrase containing sub-phrases. This would be used in determining the meaning of the sentence in a translation program. Programmers who work with artificial intelligence and language use these sorts of trees.
6. A parts program to locate, order and track a part of a car would be a candidate for a tree data structure.
7. Most data structures that require fast access and sorting are built using trees. For instance, we'll see that many of our subsequent data structures such as maps, sets, and priority queues all use trees as an underlying foundation.

Of the above list, items 3, 5 and 7 differ from the others. They show a tree as a means, not an end. As with all data structures, we sometimes use a tree because it is helpful to solve a problem (search, sort, etc.), not because we really have an intrinsic set of data in that particular form. Bullet items 1, 2, 4 and 6 have data that must be stored somewhat permanently, and the tree really is the structure of the data. Items 3, 5 and 7, however will create the structures just to make something else work, not because the data really is in a tree form, intrinsically.

4A.1.3 General Tree Design Strategy

In the study of tree data structures, our journey begins with the most general and ill-behaved type of tree. It is so ill-behaved, it doesn't even have a name. We just call it a general tree, or tree, and reserve all the cool words (like binary search tree, AVL tree, etc.) for certain sub-types that have structures which make specialized operations easier to implement. But the general tree, as wild and challenging as it is, is worth studying because sometimes that's what we're handed, and we have to have an idea of how to face it. And it does, after all, represent many of the types of applications listed above.

This most general tree can have nodes with variable numbers of children. Here is such a tree, in its logical from:

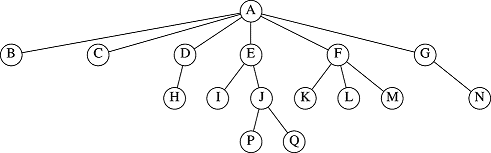
If I were to ask you to implement a tree data structure that supported some of the typical operations like addChild(), removeNode(), find() and print_all(), I would probably get some interesting and creative answers. Some such solutions might attempt to define a TreeNode with a dynamic array of pointers to children. If a TreeNode had three children, then we might allocate a vector of three child TreeNodes. Of course when we add or delete children, this would require resizing the vector. There is, however, a smarter and more accepted method for lashing up these beasts which is quite flexible and more efficient than the vector approach. It entails giving each TreeNode a structure almost identical with our list nodes: data plus two pointers. However, instead of the pointers being next and prev, the pointers are firstChild and sib (meaning next sibling) This would cause the above logical tree to be stored, in reality, in the following manner:

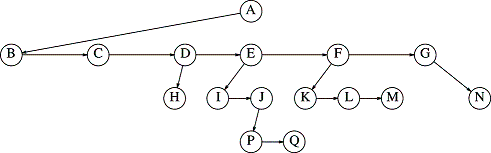
To understand how this relates to the TreeNode type I described, consider a few of the nodes above:

• TreeNode A: firstChild points to B, sib is NULL
• TreeNode C: firstChild is NULL, sib points to D
• TreeNode E: firstChild points to I, sib points to F
• TreeNode H and Q (among others): firstChild is NULL, sib is NULL

4A.1.4 General Tree Implementation

Before jumping in, let's imagine an operation like removeNode(). Removing TreeNodes -- I mean really removing them, not just marking them as deleted -- is one of the trickiest operations to implement in a tree ADT. What would this look like? First, it would be a member function - an instance method -- of our tree template. This means we'd call it using a tree object:

   myTree.removeNode( ... );

What goes into the argument list? One idea is that we would pass it a TreeNode*, that is a pointer to our basic node type. Imagine we somehow got our hands on a pointer to nodeK in the above diagram. Call it node_K_ptr. If we wanted to remove nodeK from the tree, the invocation might look like this:

   myTree.removeNode( node_K_ptr );

Imagine, in the implementation of removeNode(), trying to move the arrows around in the above diagram to make this happen. Somewhere along the line, you would see that you need to point "around" node K, so that its parent, node F, must be modified to make its firstChild pointer point to node L. The problem, of course, is node_K_ptr, cannot be used to access node F. The best we can do with node_K_ptr is to point either the right, to node K's sibling, or down to node K's first child (if either or both exist). But that doesn't help us fix node F.

We ran into this problem with linked lists and solved it by using a doubly linked list. If we want to make use of that idea now, we would add a pointer to our proposed TreeNode class so that it now contained data plus three pointers, sib, firstChild and prev. prev would point back to the node pointing to it in the implementation diagram:

• TreeNode E: prev points to D
• TreeNode K: prev points to F
• TreeNode J: prev points to I

We are ready to take on the task of writing this template class, which we'll call FHtree. As before, we first define the FHtreeNode class.

To demonstrate an alternative to our previous technique with FHlist, I will not embed the FHtreeNode type within the FHtree template, but make it a separate data template, defined along side the FHtree. The form, within the include file, FHtree.h will be like so:

template <class Object>
class FHtreeNode
{
   friend class FHtree<Object>;
 ...
};
 
template <class Object>
class FHtree
{
 ...
 private:
   FHtreeNode<Object> *mRoot;
};

The effect is notationally simpler. The client, rather than using the scoping operator, will define the FHtree objects and any needed FHtreeNode objects separately:

#include "FHtree.h"
#include "iTunes.h"

int main()
{
   FHtree<iTunesEntry> tunesTree;
   FHtreeNode<iTunesEntry> *tn;
    ...

I'll make a few comments before we start writing code.

• We will not use iterators. Because it is unclear what, exactly, an iterator would do -- move to the next sib? or move to a child? -- we would have to spend too much time defining different sorts of iterators and iteration operations. It just would not pay, alogorithmically. Instead, we use simple pointers to the individual FHtreeNodes when we have to point to a node in the tree.
• You might think that we could somehow build the tree structure on top of STD lists or FHlists. No such luck. Again, the work that would be required to do even this, is unwieldy. These general trees are just too amorphous to yield a neat solution based on a plain doubly linked list. You are free to try on your own.
• As you read these function implementations, note how recursion is used. Recursion is a very common technique in trees because here it does not result in significant overhead. You can do the algorithmic analysis on a case-by-case basis, but it usually involves a minor price increase, and if it matters, there are ways around it.
• It's not necessary to follow every detail of every algorithm. However, pick a few and do make an effort to fully understand those. See if you can modify it to work better, faster, smaller. It's good for your programming skills.

4A.1.5 FHtreeNode

The FHtreeNode is very short. Here is the main part, with a couple items removed to make it clearer for the lesson:

template <class Object>
class FHtreeNode
{
   friend class FHtree<Object>;

private: 
   FHtreeNode *firstChild, *sib, *prev;
   Object data;
   const FHtreeNode *myRoot;  // needed to test for certain error

public:
   // constructor that takes an Object and some node pointers
   FHtreeNode( ... )
   { }

   // ... a couple others

}; 

We declare FHtree to be a friend. This enables FHtree algorithms to get to FHtreeNode data without restriction.

As advertized, we have three pointers and a data member. However, there is an extra pointer that I didn't mention: myRoot. Can you guess what this one does? It is similar to the my_list member of the list::iterator. We will use it to guarantee that we are not trying to use a tree A node pointer in a tree B operation. Remember this:

   myTree.removeNode( nodeKPtr );

We have to protect ourselves from an evil client passing in a nodeKPtr which points to a node that does not belong to myTree. The myRoot pointer will help with that, as every FHtreeNode will point to the root of the tree to which it belongs. We can then test the FHtreeNode argument passed in to this function, comparing its myRoot pointer to the mRoot member of the calling object (we define mRoot in FHtree next).

4A.1.6 FHtree Prototype

We complete this section by looking at a representative part of the FHtree class prototype. It is not too scary looking.

template <class Object>
class FHtree
{
private:
   int mSize;
   FHtreeNode<Object>  *mRoot;

public:
   FHtree() { mSize = 0; mRoot = NULL; }
   ~FHtree() { clear(); }

   // several items not shown.   
   FHtreeNode<Object> *addChild( FHtreeNode<Object>  *treeNode, const Object &x );

   FHtreeNode<Object> *find(const Object &x) { return find(mRoot, x); }
   
   FHtreeNode<Object> *find(
      FHtreeNode<Object>  *root, const Object &x, int level = 0);

};

Private Members and Constructor

You can see the private members, mSize and mRoot, as expected. The constructor sets mRoot to NULL, which tells you that we are not using any "header nodes" to our tree. Header nodes don't confer the same advantage to tree algorithms, as they did in linear list algorithms, so there is no reason to have them here. The destructor calls a method, clear(), whose prototype is not shown, but it basically deletes all the nodes in the tree

addChild()

Here we are taking an Object &, x, which is the intrinsic type-parameter of the instantiated (or perhaps we should say "specialized" because this is a template not a class) FHtree. The method will wrap x in an FHtreeNode object (allocated in the function) and link-it-in the tree as a child of the tree node which is also passed in as a parameter. In other words, this method can only be used after the client has identified a particular tree node in the tree that represents where we wish to place our Object -- this treeNode will be the parent of the new object.

The way this will work in practice is that we will use a method find(), described next, that will search for an Object in the tree and return a pointer to the tree node that contains it.

The two find()s

This next part is very important so you must understand it thoroughly. In many recursive implementations, trees being a major example, the client will often call a public member function . However, that public function will go on to call a nearly identical, overloaded, version of itself that takes extra parameters. These extra parameters control the recursion; they change as the call is repeated downward, bringing the recursive calls closer to some terminal non-recursive case. Here, we have two find() methods, one that takes the Object that we wish to find, and a second overloaded variant that takes that Object together with a treeNode pointer which represents the root of the subtree in which we are looking. Initially, the subtree that we are searching is the whole tree, as we see by noting that the first call to the overloaded find() passes mRoot as the extra parameter. What you will see when we study the implementation of find() is that every recursive call will change the parameter root to move it further down the tree toward its leafs, so that we are searching in an ever shrinking tree. Eventually we find the Object (or reach a NULL). When we do, we pass the FHtreeNode pointer where it lives (or the NULL) back up to the original call.

This is a theme in recursion, and you will see pairs of functions, the public version and the more technical, often private version. It is crucial that you understand why this is done and that it must be done.

This overloaded variation is usually private in most data structures since it is not good form to allow the client such technical access to it through these extra parameters. However, in our FHtree, we will find that it is useful to let the client search for something in some subtree that it has already identified. For example, there may be several "left arm" objects in the tree, one that belongs to "Carlo", one that belongs to "Singh", one that belongs to "Nana", and so on. So we first find the node that points to Carlo:

   FHtreeNode *tn = sceneTree.find("Carlo");

The returned FHtreeNode pointer now identifies the portion of the tree that defines "Carlo" and it is in this subtree that we wish to search. From there, we can start our search for "left arm":

   tn = sceneTree.find(tn, "left arm");

Note the first find() invocation uses the simpler variant that takes no subtree parameter and starts from the root, but the second find() invocation uses the more detailed variant and thus starts from a subtree of interest.

By the way, the int parameter, level, is not important to this discussion so I am ignoring it here.

This is an overview of a general tree. Next I'll show you how to implement a find() and a few other methods of the FHtree. You will, of course, receive a complete include file that you can play with, FHtree.h.