Section 3 - Exponential Running Times

3B.3.1 fibonacci: Bad Use of Recursion

Now we come to the worst use of recursion imaginable -- the computation of the Nth fibonacci number. The fibonacci numbers are defined as a sequence where the Nth number is the sum of the N-1st and N-2nd. In other words, the sequence is:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...

We express this formulaically:

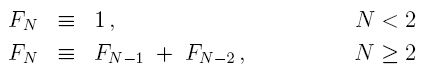
The definition is recursive, but that doesn't mean the implementation should be. Let's do it the wrong way, then analyze it.

int fib(int n)
{
   if (n > 1)
      return fib(n-1) + fib(n-2);
   else
      return 1;
}

The irony is that, looking at the above, it seems so elegant. An unsuspecting and aspiring programmer might feel proud to have discovered this solution, but now we have to be critical of it. To understand how bad this is, first, without analyzing the situation, but just using your gut, how high do you think N has to go before this algorithm takes longer than 10 seconds on a fast computer? 1 million? 20,000? Secondly, if you increment N by 1 (say from N = 45 to N = 46) do you think that it would be remotely possible to even experience a difference in the running time? This is not intuitive. It seems that we could take fib( 1 million ) easily in under 10 seconds using this function. Also, certainly there should be no discernable difference between fib(45) and fib(46). Both of these statements are wrong.

The program that times this is easy enough to write:

// --------------- main ---------------
int main()
{
   int k, result;
   double elapsedTime = 0;
   clock_t startTime, stopTime;

   for ( k = 20; elapsedTime < 10 ; k++)
   {

      startTime = clock();    // start timing ---------------

      result = fib(k);

      stopTime = clock();      // stop timing ------------------------
      elapsedTime = (double)(stopTime - startTime)/(double)CLOCKS_PER_SEC;
      cout << "fib(" << k << ") =  " << result << endl;
      cout << "N: " << k << ", Running time: " 
         << elapsedTime  << " seconds" << endl << endl;
   }
   return 0; 
}

And we now publish our shocking results:

 ...
 
fib(41) =  267914296
N: 41, Running time: 1.232 seconds

fib(42) =  433494437
N: 42, Running time: 1.997 seconds

fib(43) =  701408733
N: 43, Running time: 3.245 seconds

fib(44) =  1134903170
N: 44, Running time: 5.241 seconds

fib(45) =  1836311903
N: 45, Running time: 8.502 seconds

fib(46) =  -1323752223
N: 46, Running time: 13.759 seconds

Press any key to continue . . .

The difference between fib(41) and fib(42) is about 60%. The difference between most consecutive computations is often above 50%. And if we want to compute fib(46), we'll have to wait five more seconds than we waited when computing fib(45).

What's happening?

3B.3.2 Exponential Running Times

Let's analyze this algorithm as we did our binary search. Because we are recursing, we can formulate an approximate running time for T(N) using the formula:

We know this because, within the call to fib(N) we are calling fib() twice, once passing N-1 and once passing N-2. The C, like before, represents the other constant-time junk that happens in each call, things we know we can ignore because of your rules about adding constants. Unlike the binary search, however, we never get out early. So we always must recurse down to the bottom, meaning our running times will not be better than some worst case, but actually equal to the worst case.

Also, I want to compute an Omega, Ω, time, not a Big-Oh time, because I suspect the result is going to be bad - and I want a lower limit (best time) rather than an upper limit. To do that, I'll replace T(N-1) with T(N-2) above, which will shorten the time giving us a lower bound. For the same reason, we'll throw away the C term. So:

Which gives us a nice formula to expand. Let's say that N is a power of 2 for simplicity. This will help us get a lower bound on the running time, an Ω, so to speak:

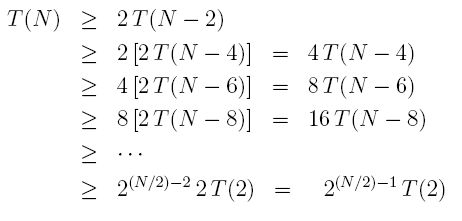
T(2) is a constant factor which we can ignore, as in all such order-of-magnitude estimates. Also, by using a constant, K = sqrt(2) instead of 2 for the base of the exponent, we can get the fraction out of the exponent, for a final result of:

This means that every time we increase N by 1, we multiply the running time by at least a factor a K = sqrt(2), which is more than 40%. Remember, because this is an Ω estimate, things might be even worse. The best it can be is a 40% slow-down every time we increase N by 1. Wow. Sloo..oo...ow.

This is what exponential running time means. It is not something to brag about.

Of course, there is a simple non-recursive function that will compute fibonacci numbers very quickly, so there is no need to worry there. The important thing is to see how bad recursion can be if we use it haphazardly.