Section 2 - Logarithmic Running Times
3B.2.1 Removing N/2 Items Each Operation Is Good
The excellent speed that we accomplish in a binary search is due to the fact that, in one constant time operation, we totally eliminate half the size of the list. To get a good idea about how quickly this will converge on a solution we have to count the number of times, worst case, that the operation must be performed. Here is the algorithm, again, for reference:
template <typename Comparable>
int binarySearch(Comparable array[], const Comparable &searchItem,
int firstIndex, int lastIndex)
{
int middleIndex, result;
if (firstIndex > lastIndex)
return -1;
middleIndex = (firstIndex + lastIndex) / 2;
if (searchItem < array[middleIndex])
return binarySearch(array, searchItem, firstIndex,
middleIndex-1);
else if (searchItem == array[middleIndex])
return middleIndex; //found him!
else
return binarySearch(array, searchItem, middleIndex+1,
lastIndex);
}
There is no loop, but there is a recursive function call. If T(N) is the time our algorithm takes to process N elements, we can see by looking at this code that T(N) = T(N/2) + C, where C represents some constant time operations. Don't take my word for it: look up. If we enter this function with an array of size N (say lastIndex - firstIndex = N), then we call the function recursively on size N/2 (middleIndex - firstIndex). So whatever time that recursive call takes, T(N/2), we add to that a few constant time tests (C) to get the full time T(N) which proves that T(N) = T(N/2) + C.
Also, what is the "deepest" we can get in any recursive call. That is, how many function calls can be on the call stack at any one time? Since each time we call the function we divide the number of items by 2 compared to the parent call, this gives us the answer. To understand that, imagine that N is a power of 2, say N = 2p, for some integer p (for example N = 256 which means p = 8). Then after, at most, p+1 recursive function calls we will be at the end case where the recursion will start to unwind. This happens either because firstIndex will be > lastIndex (if you divide 256 by 2 eight times, you get down to 1) or we will have found the item. (It is a counting detail that we might have to call the function p+1 times rather than p, and adding 1 does not change a running time calculation, so I will simplify in what follows to say that we only call the function p times in worst case).
Let's apply the relation
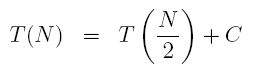
until the recursion ends:
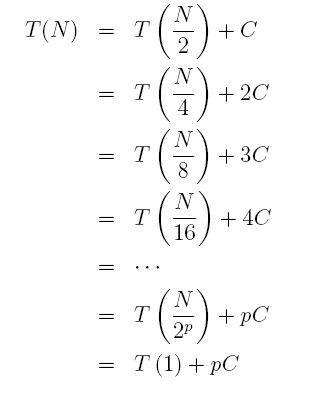
But p = log2N (because N = 2p) which tells us:
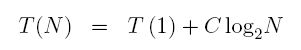
Now, this is really an upper bound, not an equality, because at any time in the above recursion, we might have ended by finding the search item. So the equality is really an inequality, namely
This is the result we suspected. It tells us that for large N, the algorithm grows no faster than log2N which is as slow as you can grow. It does not matter too much that we are using log base 2 or log base 10 or log base 16, so we summarize the result using:
This is what logarithmic running time means. So if we are processing, say, 32,000 elements, we are done in about 16 operations. Pretty fast.
This can be summarized into the following rule:
TipAny time a task can remove a fixed fraction of the collection in a constant time operation, it has, at worst, logarithmic (or log) running time.
Note the key word, fixed. This means that there is some fraction, like 3/7 which reduces the list each time. It doesn't matter how small the fraction is, as long as it's fixed and not a function of N. In this case, the fraction was 1/2. Also, the entire binary search algorithm was represented by this one task so the algorithm is logarithmic There might be some algorithms in which the task is only part of the algorithm. For instance if the algorithmic task occurs within a loop which has O(N) running time, then we must, as usual, multiply the log time by N to get the final running time of O(NlogN).
Sometimes it's hard to measure log running times directly because they are so fast. The way to do it in such situations is to embed the search in a loop that occurs, say, 1000 times. Then you could get a non-zero value which represents 1000 times the true running time. Still, each time we double the size of the array, the magnified running time should increase by a tiny fixed amount, not obviously dependent on logN.