Section 4 - Theta Estimations From Code
3A.4.1 Counting Big-Oh More Accurately
The estimates so far were upper bounds, and might not represent the true algorithmic performance. Maybe we put too large an upper bound on our code. For example, when we estimated the bubble sort, we counted the inner loop as O(N) even though it did not do the loop N times, but top times, which was, only N-1 once, and had smaller values as the algorithm proceeded. Maybe using N for that loop was wrong for getting a snug fit on the upper estimate.
Here is a shortened view of the entire sort algorithm in a single function format. To keep things easy, I have removed the boolean test which allows us to escape early (we can do that, since we are considering worst case, and that means we never "escape early".
for (int k = 0; k < arraySize; k++)
for (int j =0; j < arraySize - 1 - k; j++)
mySwap(data[j], data[j+1]);
In our Big-Oh estimate, we counted the inner loop as N since we knew that its longest pass was N-1 and we were looking for an upper bound. But now, let's count a little more precisely. Ignoring the -1 in the inner loop, since it doesn't really matter, the inner loop counts to N - k and the outer loop counts to N. So a better estimate on the timing of this loop is as follows:
Rearrange the sum so all the Ns come first and the 1 + 2 + ... come after, and you get
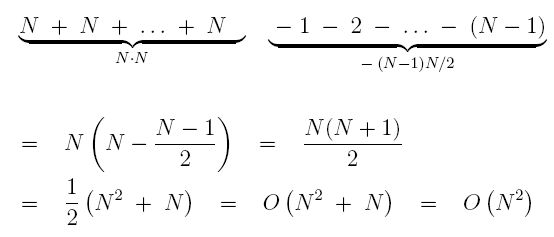
We see that even if we count more accurately, we still get O(N2).
What we learned is that even if we perform a tighter estimate, we still end up with the bubble sort being O(N2) which is to say it has Big-Oh time complexity O(N2). This makes us believe that we really do have the smallest upper bound that we can get. Maybe this is a theta estimate, after all.
3A.4.2 Counting Ω And Θ
If you were to do a similar analysis, but this time think about the minimum rather than the maximum number of operations, you would still get something very close to (1/2)N*N. Each time you did a simplification, rather than over-estimating, you would underestimate. You might find that the you'd need a smaller constant (something less than 1/2) but it would still be a constant times N2 Thus, we would see that Tbubble sort(N) = O(N2) and Tbubble sort(N) = Ω(N2). Thus, Tbubble sort(N) = Θ(N2).
You don't really need to do this, in practice. If you are careful in your Big-Oh estimations and always use the lowest upper bound that you need, you will naturally come out with the Θ estimates. It is good to know the techniques, though, if you ever need to really be certain about the results.
3A.4.3 Final Note on Bubble Sort: If Statements
We briefly disposed of the if statement that lets us out of our inner loop early in case we find that, mid algorithm, we have a sorted list. The results for Big-Oh don't change, though. In the case of an if statement, we must take the worst case, always. That's what Big-Oh means. So, Tbubble sort(N) = O(N2), even with the full algorithm and this is the best we can do. On the other hand, the Ω estimate would use the shorter of the two options in an if statement, and if you did that, you would end up seeing that Tbubble sort(N) = Ω(N) and you could not really improve on that. Here, we need to look at the average cost of the algorithm, and for that, we make an assumption. (Practically any assumption we make would give the same result). If we assume that we break out of the inner loop half way through and also that our list is sorted half way through the outer loop, we still end up with a running time of Θ(N2). You can count this yourself using the earlier computations as models.
3A.4.4 The Executive Summary
The big picture is pretty easy for simple nested structures. If you are looking at an algorithm, find the deepest nesting structure - that's the only one that counts. If each loop (or function call) is dependent on N, then the number of nesting levels is the exponent of N in your Big-Oh or Theta estimate. Since the insertion algorithm had one loop, it was O(N). Since the bubble sort had two nested loops on its interior, it was O(N2).
To see if you understand these ideas, outline the following three algorithms in your mind or on paper, and figure out the what orders their running time are:
- Addition of two N×M matrices.
- Matrix multiplication of an N×N matrix.
- Searching for a string in an array of N strings.
- Searching for an iTunesEntry in an array of NiTunesEntry.
If you don't know what matrix multiplication is, now's a good time to find the definition on the web or in a math book.