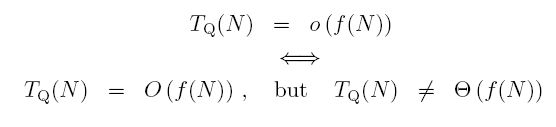Section 2 - Getting a Tighter Fix on Growth Rates

3A.2.1 Lower Growth Bounds: Ω

We define a lower bound for growth rates, now. We express the fact that an algorithm Q is said to grow faster (or at least no more slowly) than some mathematical expression f(N) (like N or N²) using the notation:

We mean that T_Q(N) grows no more slowly than f(N). This time, we are giving our timing on algorithm Q a lower bound using the function f(N). In words, we say "the timing for algorithm Q is omega f(N)". This technical definition of "grows no more slowly than" is similar to its counterpart, in Big-Oh terminology, to wit:

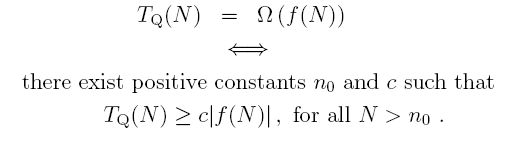
This means that while T_Q(N) might start out being much smaller than f(N) for small N, eventually we are guaranteed that this will settle down as N increases, and T_Q(N) will never be less than cf(N ) for large N.

3A.2.2 Exact Growth: Θ

Finally, we express the fact that an algorithm Q is said to grow at exactly (a term which is not universally used, because it could be misinterpreted) the same rate as some mathematical expression f(N) (like N or N²) using the notation:

We mean that T_Q(N) grows neither faster nor slower than f(N). In words, we say "the timing for algorithm Q is theta f(N)".

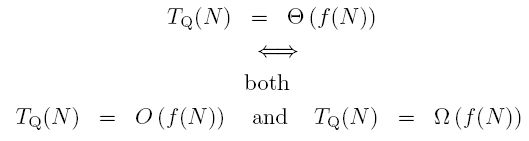
This is, ideally, what we want to know about an algorithm. Normally, when programmers informally say an algorithm is Big-Oh of N, they really mean that it is theta of N, because they have actually narrowed down the growth rate to being precisely linear.

Typically, when we compute a growth rate for an algorithm, we'll compute a worst case scenario. That worst case will give us a Big-Oh value, but also, it says that if the algorithm is continually faced with a worst case scenario, then this is the growth rate, namely, it is a theta value.

3A.2.3 Little-Oh

Less frequently, you may come across Little-Oh notation, that is, T_Q(N) = o(f(N)). This simply means that we not only have an upper bound in f(N), but this upper bound is, in some sense, too high. One way to say this is that