Section 1 - Linked Lists

2B.1.1 Singly Linked Lists

You have seen linked-lists (or just lists) before in one guise or another. A list is a collection of Nodes, each Node consisting of two members:

• data (whose type could be anything - string, iTunesEntry, int, etc.), and
• a Node pointer, usually named next.

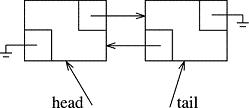
Our only access to the list is through a Node* often named head. We end up creating two classes if we want to implement a list. First, we define a Node class that describes a single Node object. Then we define the actual List, which, ironically, is almost nothing - it is just a single pointer to the head of the list. Here is the picture:

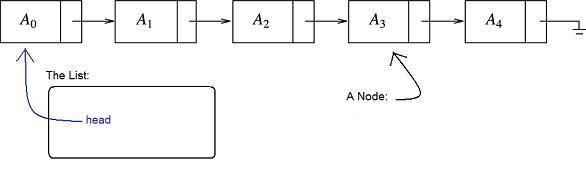
The Node data in the above pictures would be the Ai, while the List would consist of the one Node *, head, along with the multitude of methods (not shown). The next pointers for each Node are represented by the arrows. We use the terms predecessor and successor to discuss Nodes to the left or right, respectively, of any given Node as depicted above.

Unlike an array, or vector, a list is fragile in that you can completely destroy it, or lose huge amounts of data, by accidentally modifying the next member of just one Node in the list. If such a pointer points away from its correct successor, we lose the entire right side of the list (i.e., everything that succeeds the offending Node). It is important to remember this and keep the above picture in your mind at all times. If you understand this idea, then you will be able to add some well-chosen members to your list class One such member often added is a second Node* usually called tail that points to the last element of the list.

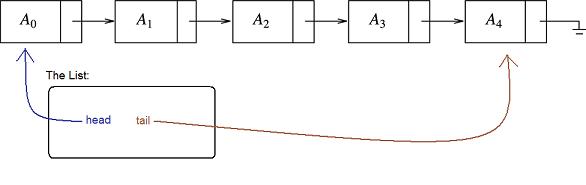
The symbol at the far right is EE-speak for "ground", but we use it here to mean NULL. That is to say, the next pointer of the last Node in the list is NULL - that's how some algorithms will know they have reached the end of the list.

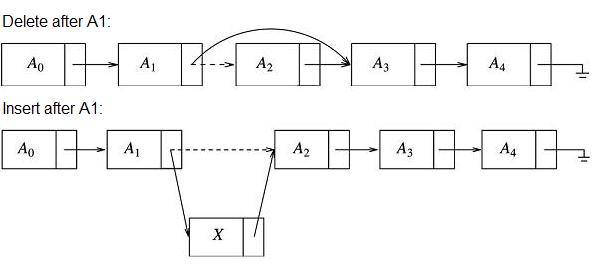
A simple list like this requires some careful machinery to manage it. We will always want the ability to add elements to the head or tail of the list; this means creating methods with names like push_front() and push_back(). We'll also want to be able to remove such elements with methods named pop_front() or pop_back(). If we wanted to insert a Node into the middle of a list (or remove a Node from the middle) we might provide an insert() or erase() method in our list class with a signature that takes the Node* to the location where we want this insertion or deletion to take place:

   void List::HypotheticalInsert(Node *nodeToInsert, Node *location);
   void List::HypotheticalDelete(Node *location);

Here we can see the links that need to be adjusted for insertion and deletion.

2B.1.2 Doubly Linked Lists

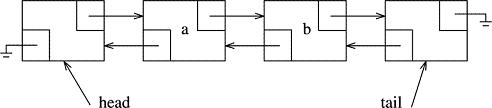
Unless space is hyper-critical, it pays to give our Node class a second pointer member called previous or prev. This will point to that Node's predecessor. With this extra datum, we can roll up and down the list more easily and even erase a Node to which we point (rather than the Node after-which we point, as would be required in a singly linked list). With two, rather than one, pointers for each Node, we have the following picture:

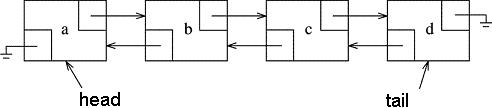
The arrows to the right represent the next pointers, and the ones to the left represent the prev pointers. The list class in this picture would consist of the two pointers head and tail. Remember - head and tail are not Nodes, they are simply pointers. The Nodes actually live outside the list class, although they are controlled by the list since it is the list class methods that will allocate the Nodes, and the list will be able to access and mutate the Nodes by starting from either the head or the tail and following the next/prev pointers forward or backward through the list.

In what follows we will find it very convenient to construct our list class objects with an empty list. However, an empty list, for us, will consist of two non-data-holding Nodes. Informally, these will be called the header and tail nodes. Here is a newly constructed, empty, list:

These two bookkeeping Nodes look just like all the other Nodes in the list, but they will not contain any data. The header node is always the first Node. We will always skip the header node when traversing the list. Similarly, the tail node is the last Node in the list. We will stop our traversal of a list just before actually processing the tail node. As shown below, there is no data in the Nodes pointed to by the list's head and tail members. These are the header and tail nodes.

Why do we have header and tail nodes? Again, if you have ever implemented a linked list, you will appreciate this: If you did not have a header node (in a singly linked list) or a header and tail (in a doubly linked list) then you had an ugly case if (head == NULL) in practically every one of your methods. This is not the only trouble you had, but it gives you the idea of the horror. Header (and tail) nodes make our work much easier.

2B.1.3 Comparing vectors with lists

While a vector takes a standard array approach to the data structure, allowing constant time random access to all data, but requiring longer time for algorithms that insert new data into the middle of the vector, lists exhibit the opposite behavior: They require more time to access individual elements in the middle of a list (because they need to search from the head or tail and follow pointers), yet the insertion of items into the list is a fast, constant-time, proposition. Another difference is that vectors will only grow new capacity in sporadic fits and starts when required, and rarely get smaller, while lists grow and shrink as needed in a smooth and continuous way at each insertion or deletion. Yet another internal difference is that vectors store all the objects internally, while lists store nothing other than a header and tail node internally, allowing bulk of the data structure to live outside the object. As we'll see, these differences determine which we will want to use to build more complex ADTs.

2B.1.4 STL lists and FHlists

Our next topic will involve rolling up our sleeves and implementing our own list. In truth, I will implement the list and you will watch. However, don't read carelessly. You may have to do this at some point in the next few weeks on a smaller scale, so read, understand, experiment with and ask about each detail.

Our approach will be to implement FHlists that work almost exactly like STL lists. By doing so we will gain insight into how STL lists work, and also have the option of doing it ourselves if we ever wish to. You will have the advantage of using the file FHlist.h which is yours to keep and modify.

After some pages of onerous and fun-filled coding and learning, we will have developed our second basic tool (after FHvectors) upon which we can build the coolest data structures and algorithms known to mankind.