Section 9 - Application to the Subset Sum Problem

1B.9.1 A Class For Sub-Lists

In order to program the algorithm for the subset sum problem, we'll need a data structure that can:

1. represent any subset of a given set, S.
2. have a method capable of generating a new subset from existing subsets.

Item 2 is needed so we can realize the following operation (from the lesson in module 1A):

If L is a subset (a.k.a. sublist or just list) of positive integers from S and x is member of S, then we let L + x denote the augmented sublist derived from L by adding (i.e. appending) xto the set L. For example, if L = {4, 1, 7} then L + 2 = {4, 1, 7, 2}

Thinking about this logically, a sublist class that will assist us should have the following features:

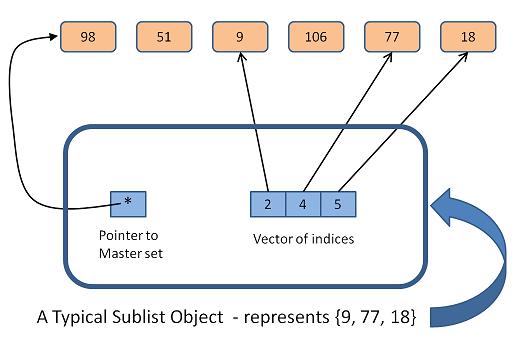
• It should store a pointer to the master set from which we are forming subsets (or sublists -- I will use the two terms interchangeably). We want a pointer because we don't want to replicate the large master set for every sublist we create.
• Each sublist object should describe which items from the master set that this sublist contains by storing its items' indices (relative to the master set). In other words, when we form a sublist, we won't actually store the selected items themselves in the sublist, but rather the indices of the items.
• It should use a vector of ints to represent the actual sublist stored. These ints are the indices of the elements in the master set from which this sublist comes.

The above can be visualized like so:

In addition, we will need some support for the algorithm:

• It should store the sum of the objects in this sublist for fast and easy access.
• It should have a way to display the elements of the sublist represented by the object.
• It should have an instance method, addItem(), that takes an item from the master set and forms an augmented sublist that has that item added to the items already in the calling ("this") sublist. It is not a mutator, however, since it will not change the this object, but rather return the augmented sublist as a functional return. The augmented sublist can start out as a local copy of the this sublist object, and then it can be modified by adding in the parameter item. It needs to also adjust the sum of the newly created sublist, since it will be larger than the sum of the this object. Finally, it returns the new sublist to the client. The method will take as a parameter the index (in the master set) of the item that is to be added to the this sublist.

Here is a prototype for such a class.

class Sublist
{
public:
   Sublist(vector<int> *orig = NULL) 
      : sum(0), originalObjects (orig) { }
   Sublist addItem( int indexOfItemToAdd );
   void showSublist() const;
   int getSum() const { return sum; }

private:
   int sum;
   vector<int> *originalObjects;
   vector<int> indices;
};

I am using int for sum, since this is all we need for our homework. If underlying objects had floating point values, then an adjustment could be easily made. The implementation details of addItem() and showSublist() are straightforward and will be left to the student.

1B.9.2 A Plan For the Algorithm

The algorithm can be implemented in main() (which is a global function, not a method of the Sublist class). Here is the abstraction, repeated from a prior lesson:

• initialize the collection Col with one sublist: the empty sub-list.
• loop over all elements x in S
  • loop over all elements, L that already are members of Col
    • if sum(L) + x < t, add the sublist L + x to Col
    • if sum(L) + x == t, break from both loops
• of the sublists that end up in Col, find the one, L', with the largest sum()

The collection Col will itself be a vector of Sublist objects. So we are using vector both inside the Sublist class and also at the client level.

I should say something about the + operator in the expression sum(L) + x. If the underlying master set is just a bunch of ints, then this is self-explanatory. However, what if the underlying set is an iTuneEntry or Widget? The + operator needs to be defined that takes an int, sum(L), and adds that to the item x. This is done by overloading + so that we actually add the numeric value within x that we are interested in. In the case of Widgets it might be a cost or weight value, while in the case of an iTuneEntry it is going to be the tune's playing time, or tuneTime, accessible through, say, x.getTime().

An ideal approach, especially in light of our eagerness to incorporate templates, would be to create a template class for the algorithm and allow the client to pass any type of master data set - not merely a collection of ints - to the template. This is possible, but presents some challenges as we will see in our first assignment.