Section 2 - Kruskal

11A.2.1 Cycles

A cycle in a graph is, loosely speaking, a path that forms a closed loop. Formally, a cycle is a sequence of edges, (v₀, v₁), (v₁, v₂), (v₂, v₃), ... , (v_N, v₀), which starts and ends at the same vertex. This definition works for both directed graphs:

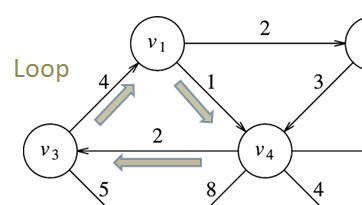
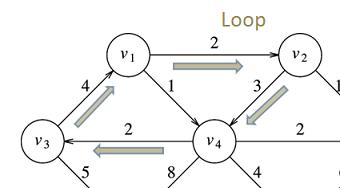
and non-directed graphs:

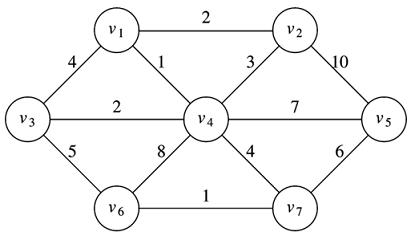
Cycles are more common in non-directed graphs because we don't have to obey arrows to find a way to loop a vertex back onto itself. The above graph contains nothing but cycles for that reason.

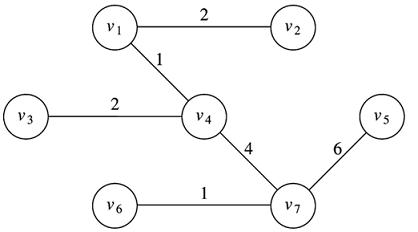
Cycles are important in minimum spanning tree algorithms because they are not allowed in the final result: If you have a cycle, then you can always eliminate one edge in that cycle and make the graph cheaper. Note that the MST of the above graph has no cycles:

Like dijkstra, kruskal is easy to describe, but then we have to make sure it really works.

We initialize two edge sets. The first, edgeHeap, comes from our input graph, G. It is a binary heap (priority queue) of edges in G. We also initialize a second set (it is not a heap, just a set) that starts out empty. This will be called newEdges and will eventually contain only the subset of edges needed for the MST. In a very simple loop, we pop off the minimum-cost edge from edgeHeap and decide whether to add it to newEdges or throw it away. To make that determination, we see if adding the edge would create a cycle in newEdges. If it would, we toss it. If not, we add it to newEdges. As soon as we notice that newEdges contains representatives from all the vertices in the graph, G (by looking at the source and destination vertices in each edge), we stop: we're done. But we only have a box of edges; so we have to build a graph out of it (in our case by sending newEdges to a conveniently available mutator setGraph() in our graph template).

Outline of Kruskal Algorithm.

That's it.

11A.2.2 Picturing Kruskal

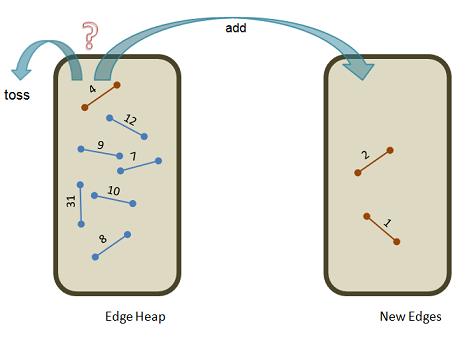
This algorithm is easy to picture since it only involves one loop and one major decision:

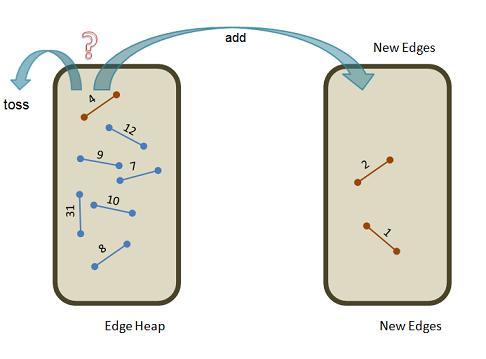
The looming question is how do we easily detect a cycle? This is done as follows. Create a collection of vertex sets, each set initially containing exactly one vertex from the original graph:

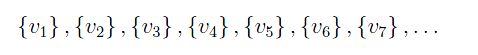
Every time we add an edge to newEdges, we combine (take the union of) the sets containing the source and destination vertices of that edge. For example, if we are just starting out and we added the edge (v, w) to newEdges, then we would take the two sets {v} and {w} and form their union, {v, w}. This would replace the two smaller sets with one larger set. Later, if we came across the edge (v, s) we would take the union of the sets {v, w} and the set {s} and form the union {v, w, s}. Each time we form a union, the number of sets decreases by one, but one of the surviving sets gets a little larger. Now, how do we detect a cycle? If we are examining an edge just popped off of edgeHeap, but before we have decided whether or not to place it in newEdges, say (w, s), and we see that w and s are already in the same set, we know we have a cycle (think about this). In that case, we toss that edge. We don't need it and we can't use it. So, we are using this collection of sets that start out as a large group of singletons (sets with only one element each), and as the algorithm progresses, we merge sets. There will come a day when there is only one set left in the collection, and all the vertices will be in it:

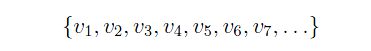
When that day comes, we know our edge set newEdges, has a minimum spanning set of edges which we can use to make a minimum spanning tree.

Here is a representation of the two edge sets in the midst of the loop. We are popping the edge with minimum cost (4) from the edgeHeap and deciding whether to add it to newEdges or toss it.

We look at its two vertices (source and dest): Let's say they are v₇ and v₂. If they happen to be in different sets in our collection vertex sets, we can add the edge:

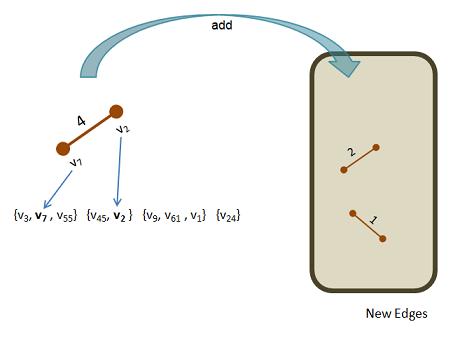
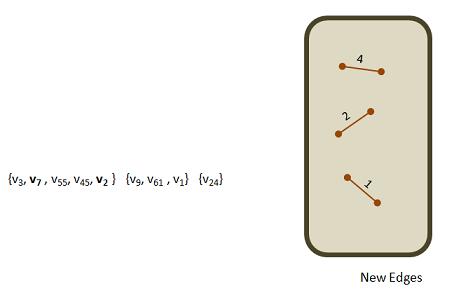
After that, we take the union of two sets and continue to the next pass of the loop. Here is the picture of the few, but larger vertex sets and the enhanced newEdges set:

On the other hand, if we had found the vertices, v₇ and v₃ in the popped edge (with cost 4), then we would notice they are already in the same vertex set:

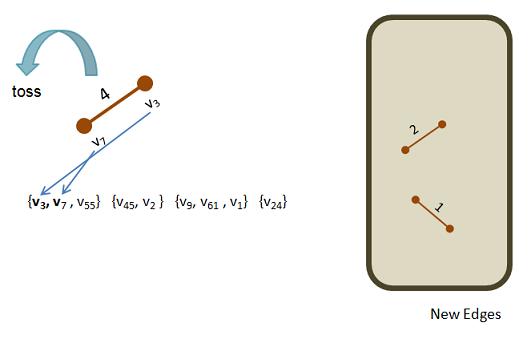
Thus, we toss the edge. Not needed, can't use it. The picture of the vertex sets and newEdges remains unchanged.

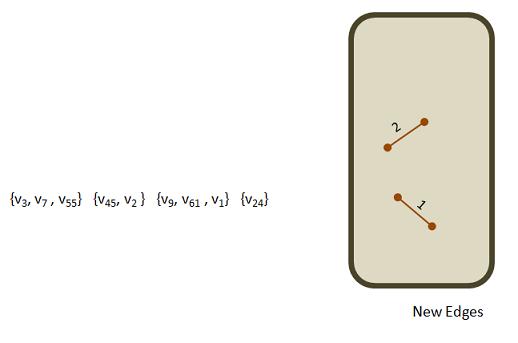
The only thing that has changed is that we have popped one edge from edgeHeap.

11A.2.3 The Revised Algorithm

Before going on, we replace the conceptual test about avoiding cycles with the concrete test where we ask if the source and dest vertices are in the same vertex set.

Kruskal Algorithm

This is pretty much all there is. We have to prove that the algorithm works, then write the code.