Section 6 - The FHgraph

10A.6.1 The FHgraph Overview

To simplify the syntax and discussion, I want to first present some typedefs that allow us to talk using simpler language. These are defined in the top of FHgraph.

   typedef FHvertex<Object, CostType> Vertex;
   typedef FHvertex<Object, CostType>* VertPtr;
   typedef map<VertPtr, CostType> EdgePairList;
   typedef set<VertPtr> VertPtrSet;
   typedef set<Vertex> VertexSet;
   typedef FHedge<Object, CostType> Edge;

We use the word Vertex instead of the more obnoxious FHvertex<Object, CostType>. We also use the two terms we have seen before, VertPtr and EdgePairList.

Next we introduce three more terms whose names describe what they are: VertPtrSet (an STL set of VertPtrs), VertexSet (an STL set of actual FHvertex objects) and Edge (a shorter name for the FHedge data type).

The data of our graph will really only be one thing: a set of vertices. This is the central idea you need to remember. I have already prepared you for the fact that a collection of our FHvertices is going to contain all the information we need in order to define the graph. That's because we included adjacency lists in the FHvertex objects themselves. So just focus on that, and you will understand the big picture. When you create your own graphs, you might borrow this notion. And if you do, there will be some C++ implementation details that must be handled, the likes of which the following discussion will reveal.

To put it simply, then, our FHgraph will principally be one single glob of data:

private:
   VertPtrSet vertPtrSet;

These will be pointers to FHvertex objects, and we use these pointers, rather than the original objects, to do our work. We need methods to construct this set from client data and display the graph in some form. The prototypes are:

   void addEdge(const Object &source, const Object &dest, CostType cost);
   void showAdjTable();

The addEdge() method will be used by the client in the simplest manner conceivable:

   myGraph1.addEdge("v1","v2", 2);

We use statements like this to build our graph from pictures on paper. This statement constructs a directed edge with source data "v1", destination data "v2" and cost 2. Note that we are passing object data, not vertices. The client has no business knowing about, nor any worries with, things as technical as FHvertex objects. It wants to build a graph using strings, Galaxies, iTunesEntries, etc. And we allow it to do so, easily. It will be our job to wrap this data into FHvertex objects and build the graph and associated adjacency lists.

showAdjTable() can be written to display the graph in various forms. Here is how we will display the graphs. The graph:

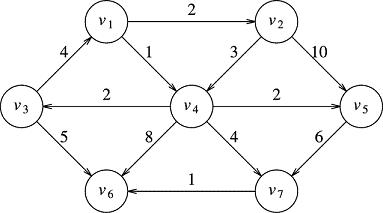
will go to the console in the following form as a result of showAdjTable():

------------------------
Adj List for v1: v2(2) v4(1)
Adj List for v2: v4(3) v5(10)
Adj List for v4: v5(2) v3(2) v6(8) v7(4)
Adj List for v5: v7(6)
Adj List for v3: v1(4) v6(5)
Adj List for v6:
Adj List for v7: v6(1)

This is our core structure for a graph. It embodies everything we need to get started.

10A.6.2 The FHgraph Data Revealed

We seek to build the data structure to support its use by a client like so:

#include <iostream>
#include <string>
#include <set>
using namespace std;

#include "FHgraph.h"

// string is the data of the vertex; int is the cost type of edges
// --------------- main ---------------
int main()
{
   // build graph
   FHgraph<string, int> myGraph1;
   myGraph1.addEdge("v1","v2", 2);    myGraph1.addEdge("v1","v4", 1); 
   myGraph1.addEdge("v2","v4", 3);    myGraph1.addEdge("v2","v5", 10); 
   myGraph1.addEdge("v3","v1", 4);    myGraph1.addEdge("v3","v6", 5); 
   myGraph1.addEdge("v4","v3", 2);    myGraph1.addEdge("v4","v5", 2); 
   myGraph1.addEdge("v4","v6", 8);    myGraph1.addEdge("v4","v7", 4); 
   myGraph1.addEdge("v5","v7", 6); 
   myGraph1.addEdge("v7","v6", 1);

   myGraph1.showAdjTable();

   return 0; 
}

The output should be:

------------------------
Adj List for v1: v2(2) v4(1)
Adj List for v2: v4(3) v5(10)
Adj List for v4: v5(2) v3(2) v6(8) v7(4)
Adj List for v5: v7(6)
Adj List for v3: v1(4) v6(5)
Adj List for v6:
Adj List for v7: v6(1)

In order to support this we will need two, not one, sets in our class:

private:
   VertPtrSet vertPtrSet;
   VertexSet vertexSet;

In order for vertPtrSet, which we already introduced, to be meaningful, we need actual vertices for the VertPtrs to point to. So we do need a set of actual Vertices. This is vertexSet. When we are asked to add an edge to the graph, we will construct two vertices, put them both into the vertexSet, then store their addresses -- pointers to these vertices -- in the pointer set, vertPtrSet. Our algorithms and other methods will use vertPtrSet, not the vertexSet, when they need vertices (for reasons mentioned earlier).

10A.6.3 showAdjTable()

Let's get our feet wet first with the easy method, showAdjTable(). This assumes that data is present in our graph. It demonstrates the use of the vertPtrSet as the principal means of access into the graph. It calls the FHvertex method showAdjList() and in fact, looks just like that method, only at a higher level. showAdjList() iterated through a map, and our present showAdjTable() iterates through a set. Please contrast and compare. This is the easy one. You can't understand what comes next if you don't, at a minimum, understand this.

template <class Object, typename CostType>
void FHgraph<Object, CostType>::showAdjTable()
{
   typename VertPtrSet::iterator iter;

   cout << "------------------------ \n";
   for (iter = vertPtrSet.begin(); iter != vertPtrSet.end(); ++iter)
      (*iter)->showAdjList();
   cout << endl;
}

10A.6.4 addEdge() and Its Helper

Now we have to get our hands a little dirty. We start with addEdge() which calls the workhorse, addToVertexSet(), the detail-oriented helper we will get to soon. At the highest level, addEdge() is used by the client to build and store a directed edge into a graph. Of course, there is no specific edge data structure within the FHgraph, but we do have to encode the information into the vertex sets and the individual vertex adjacency lists.

template <class Object, typename CostType>
void FHgraph<Object, CostType>::addEdge(
   const Object &source, const Object &dest, CostType cost )
{
   VertPtr src, dst;

   // put both source and dest into vertex list(s) if not already there
   src = addToVertexSet(source);
   dst = addToVertexSet(dest);

   // add dest to source's adjacency list
   src->addToAdjList(dst, cost);
}

What do we see? We are getting two objects source and dest as arguments from the client. The game is to wrap them each into an FHvertex object and add them, and their pointers, to our two internal sets. Once we do that, we need to place dest into source's adjacency list. That's the big picture.

The implementation is short, as shown above. Evidently, all the work is being done by addToVertexSet(). What can we infer from the two calls:

   src = addToVertexSet(source);
   dst = addToVertexSet(dest);

? Answer: we can infer that the mysterious and powerful function, addToVertexSet() must be doing the following:

1. instantiating an FHvertex object internally which will hold the client data.
2. putting the newly allocated FHvertex object and its pointer into their respective sets in the graph.
3. returning a pointer to the constructed FHvertex so we can use it for our subsequent call src->addToAdjList(dst, cost);

Now we come to the tricky one, addToVertexSet(). Here it is:

template <class Object, typename CostType>
FHvertex<Object, CostType>* FHgraph<Object, CostType>::addToVertexSet(
   const Object & object)
{
   pair<typename VertexSet::iterator, bool> retVal;
   VertPtr vPtr;

   // save sort key for client
   Vertex::pushSortKey();
   Vertex::setSortType(Vertex::SORT_BY_DATA);

   // build and insert vertex into master list
   retVal = vertexSet.insert( Vertex(object) );

   // get pointer to this vertex and put into vert pointer list
   vPtr = (VertPtr)&*retVal.first;
   vertPtrSet.insert(vPtr);

   Vertex::popSortKey();  // restore client sort key
   return vPtr;
}

Your understanding of this method relies on your understanding of STL's set::insert(), which you may have to review from last week. I'll assume that you can find and refer to our discussion on insert() and the return pair of that method.

First, we push the sort key -- the FHvertex static int that determines how < is defined. This is so we don't destroy the client's requested sort key, just in case they set and need it. We set the sort type to SORT_BY_DATA. That's because we are adding an FHvertex into our VertexSet and we do not want duplicates, that is, two vertices with the same data member.

Next, using temporary, anonymous instantiation, we build a Vertex object and (attempt to) insert it into the vertexSet. A subtle but crucial observation is that using a temporary object (or, if you prefer to avoid temporary anonymous objects, a local object variable) is acceptable. The reason for this is that a copy of the object is stored in the set, and once that happens, we can forget about the local or anonymous argument that was used in the insert().

We then come to the two lines that are pretty ugly:

   vPtr = (VertPtr)&*retVal.first;
   vertPtrSet.insert(vPtr);

The purpose of these lines is to get a pointer to the actual object, which is stored in the vertexSet, and then store that pointer into the vertPtrSet. The way this is done is by looking at retVal, the return value from insert(). Its first member contains an iterator to the object in the set, regardless of how it got there (i.e., either from a successful insert() just now, or from the vertex that was already in the set, preventing insert() from being successful). Whatever the outcome of the insert() call, retVal.first will be the iterator to the desired vertex object. We have to dereference the iterator with * to turn it into an actual FHvertex, then we need to get its address using &, because, after all, our goal is to store the pointer to the vertex.

Why do we typecast with (VertPtr)?

Although some compilers will not require it, typecasting here is technically the correct thing to do (and some compilers do require it). The pointer that retVal contains in position first a const pointer. You don't really see that directly from C++ docs, but it's an artifact of all the set, pair and insert() machinery in STL. Meanwhile, vPtr is not, and cannot be, a const pointer. It has to be returned as a mutable pointer by addToVertexSet() to its caller (which happens to be addEdge()), and that caller relies on this pointer being mutable. We are going to be using this pointer to mutate an FHvertex object that is already stored in an STL set.

Long story short, we need the typecast using (VertPtr) to get around the fact that insert() returned a pair that had a const pointer in position first.

Finally, we restore the sort key and return the pointer to the newly (or previously) inserted vertex.

10A.6.5 The Full Class

This is everything we need to satisfy the client main() above. Here is the full class, minus a few items we don't need until we consider the Dijkstra and Kruskal algorithms later in the week.

template <class Object, typename CostType>
class FHgraph
{
   // internal typedefs to simplify syntax
   typedef FHvertex<Object, CostType> Vertex;
   typedef FHvertex<Object, CostType>* VertPtr;
   typedef map<VertPtr, CostType> EdgePairList;
   typedef set<VertPtr> VertPtrSet;
   typedef set<Vertex> VertexSet;
   typedef FHedge<Object, CostType> Edge;

private:
   VertPtrSet vertPtrSet;
   VertexSet vertexSet;

public:
   FHgraph () {}
   void addEdge(const Object &source, const Object &dest, CostType cost);
   VertPtr addToVertexSet(const Object & object);
   void showAdjTable();
   void clear();
};

template <class Object, typename CostType>
FHvertex<Object, CostType>* FHgraph<Object, CostType>::addToVertexSet(
   const Object & object)
{
   pair<typename VertexSet::iterator, bool> retVal;
   VertPtr vPtr;

   // save sort key for client
   Vertex::pushSortKey();
   Vertex::setSortType(Vertex::SORT_BY_DATA);

   // build and insert vertex int master list
   retVal = vertexSet.insert( Vertex(object) );

   // get pointer to this vertex and put into vert pointer list
   vPtr = (VertPtr)&*retVal.first;
   vertPtrSet.insert(vPtr);

   Vertex::popSortKey();  // restore client sort key
   return vPtr;
}

template <class Object, typename CostType>
void FHgraph<Object, CostType>::clear()
{
   vertexSet.clear();
   vertPtrSet.clear();
}

template <class Object, typename CostType>
void FHgraph<Object, CostType>::addEdge(
   const Object &source, const Object &dest, CostType cost )
{
   VertPtr src, dst;

   // put both source and dest into vertex list(s) if not already there
   src = addToVertexSet(source);
   dst = addToVertexSet(dest);

   // add dest to source's adjacency list
   src->addToAdjList(dst, cost);
}

template <class Object, typename CostType>
void FHgraph<Object, CostType>::showAdjTable()
{
   typename VertPtrSet::iterator iter;

   cout << "------------------------ \n";
   for (iter = vertPtrSet.begin(); iter != vertPtrSet.end(); ++iter)
      (*iter)->showAdjList();
   cout << endl;
}

With this we are fully capable of defining and constructing graphs.