Section 4 - The FHvertex
10A.4.1 The FHvertex Object Overview
This is a good time to remind everyone that graph data structures are so intimately tied into the specific algorithm that is being written, the classes or templates are often custom built for each algorithm. Nevertheless, we are going to create some data structures that can be used with multiple algorithms, and we will build them using C++ classes and clients.
We begin with the vertex. Our template, called FHvertex, will have the following general contents:
- The data that the vertex represents (i.e., a reference to it).
- A vertex's adjacency list.
- A few algorithm-supporting members (one or two ints or pointers) that might be useful for various graph algorithms.
Item 1 is self-evident.
Item 2 is often not included in a vertex data structure. A vertex, after all, might live in a vacuum, and it is not until we define its host graph that we have to worry about an adjacency list. However, vertices, by themselves, aren't good for anything, so we anticipate the reality that each vertex will appear in some graph and prepare for that fact now. By making this decision, we no longer have to worry about creating an edge list in our graphs, nor will we have to have any new data members (other than vertices) in our graphs. The vertices will have the full survival kit we need.
Item 3 will not mean a lot until you get to a real algorithm, but I can give you a preview. A shortest path algorithm takes as input a graph and a single reference vertex which it uses as the starting point to measure possible shortest paths. That algorithm will compute the shortest distance from that reference vertex to all other vertices in the graph. This is a number (float or int) which will be convenient to store with all the vertices. It is very common to have a place in each vertex to store this number. We call it dist, for "distance", and it is interpreted as the distance from itself to the reference vertex. During the algorithm, this number may change until its final value rests at the true value. (Note: don't confuse this with the edge cost, an entirely different number, stored elsewhere, and one which we will get to soon.)
One member which we will not need, but that is used by some authors is a bool called completed or known. This is used by algorithms to help it know whether it has exploited the information in that vertex yet.
Because we are using some temporary storage in the form of STL sets, priority_queues and stacks, this completed member is not going to be needed; the fact that a vertex is "known" will be evident by its presence or absence in some dynamically changing set, and I do not include it in FHvertex.
10A.4.2 The Adjacency List: "EdgePairList"
The adjacency list for a vertex has to be able to, itself, contain a collection of pairs. That is, each item in this list consists of two things: a vertex and a cost. This sounds a lot like an STL pair, and, in effect that is what we'll use. However, rather than use the pair template directly, we can kill two birds with one stone. We'll use an STL map for this list, since map elements are inherently pairs. We will then create a map of vertex-cost pairs. The map template has advantages that make it perfect for this class:
- map does not allow duplicate keys. Since our vertex (the first element in the pair) will be the key value, we can toss a vertex into the list without worrying if we have already done so - map's insertion operator (adjList[neighbor] = cost) will prevent duplicates, that is, two copies of vertex == neighbor, from appearing in the same list (although it can modify neighbor's cost if neighbor is already in the adjacency list).
- map uses pairs inherently, and that's what we have.
- map is fast - logN access time (since maps and sets are both implemented using a balanced search tree, internally).
- maps do not require any client coding to find an element somewhere in the list.
Here are the first few lines of FHvertex. You see the type definition of the adjacency list, which I am calling EdgePairList:
template <class Object, typename CostType>
class FHvertex
{
// internal typedefs to simplify syntax
typedef FHvertex<Object, CostType>* VertPtr;
typedef map<VertPtr, CostType> EdgePairList;
There are two type parameters, Object and CostType. Object is, as always, the underlying data type being considered. We will use string in our clients to test our code. CostType will be whatever numeric type the client wants to use for edge costs. We will use ints in our examples, but some clients might want to use floats or doubles.
We are first defining a type that will be used often enough to warrant its own type name: VertPtr. As its name implies, it is a pointer to an FHvertex. We will use VertPtrs, rather than the entire FHvertex objects, for most of the data structure. In other words, while we will store an entire FHvertex somewhere (else), after doing so we will manipulate pointers to it, rather than the actual FHvertex object, in our secondary data structures. It is common to do this in C++ data-building. Advantages of using pointers are:
- Two pointers that are the same, really refer to the same underlying object, and the simple == operator, already defined for pointers, tests this fact. We don't have to worry about two "similar" objects being called equal. When two pointers test as equal, they really do refer to the exact same object (the one to which they point).
- There is no constructor allocation done when we have pointers embedded in larger structures like maps. This keeps the code efficient without unexpected side effects.
- There is only going to be one master object to which each pointer (for it) points. We are not going to be storing several copies of the same FHvertex.
This explains the use of the use of FHvertex* as part of many of our up-coming data structures. When we want to use one, we will use the typedef-ed term, VertPtr to define it.
The second typedef is that which will embody our adjacency list, namely map<VertPtr, CostType>. This establishes a set of vertex-cost pairs, in the form of VertPtrs and associated costs. VertPtr was just explained - it is an FHvertex* to some vertex. The second element of the pair will be the number representing the cost of that edge.
Remember the big picture here. From our above discussion, we know we are going to have a vertex point to its adjacency list, and that list consists of a set of vertex-cost pairs. The vertices in the list are the destinations of the various edges that have our base vertex as a source. A client or member method might define an FHvertex as follows:
FHvertex<string, int> v3;
This will establish v3 as a vertex. Later in the program or algorithm, we can give v3 some data using a mutator v3.setData("v3"), and even add vertices to its adjacency list, all of which will have v3 as the source. Maybe, we'll do this using a syntax like v3.addToAdjList( &v1, 4 ) and then, v3.addToAdjList( &v6, 5 ). This would add both v1 and v6 to v3's adjacency list. You can compare this little scenario with the picture:
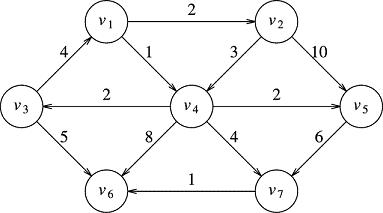
This is not exactly what we will do, but it tells you the intention of the EdgepairList in each FHvertex object. It will be a direct embodiment of the picture:

The actual EdgepairList for v3 would have a map with two elements, then. One would be a pointer to v1 and the number 4, and the other would be a pointer to v6 and the number 5. (The order of the two pairs is irrelevant. This is a map not a linked list or an ordered data structure.) This will represent the presence of the two directed edges (v3, v1) and (v3, v6) in our graph. Take a moment to get comfortable with this concept.
Here is a more complete list of the members of FHvertex (but not completely complete!):
EdgePairList adjList; Object data; CostType dist; VertPtr nextInPath; // used for client-specific info
You see the adjacency list, defined as type EdgePairList. You see the data. You see two other members representing the algorithm-specific members that will be helpful for our graph algorithms, dist and nextInPath. There is no need to discuss them here other than to say that they will be used during the implementation of one or more algorithms.
10A.4.3 The Constructor
In actuality, we will not provide a mutator, but declare everything to be public (and allow a client to manually change members). This is fine - our clients are going to be classes, not the end-user-client. Also, we will provide a constructor as follows:
template <class Object, typename CostType>
FHvertex<Object, CostType>::FHvertex( const Object & x)
: data(x), dist((CostType)INFINITY),
nextInPath(NULL)
{
// nothing to do
}
INFINITY is a large number that is defined in the class elsewhere.
10A.4.4 Adding To The Adjacency List
Now you can see how easy the addition of a vertex to the adjacency list is, using maps:
template <class Object, typename CostType>
void FHvertex<Object, CostType>::addToAdjList
(FHvertex<Object, CostType> *neighbor, CostType cost)
{
adjList[neighbor] = cost;
}
The use of map notation allows the immediate inclusion of the pair into the map and automatically protects against duplicates. Very simple.
10A.4.5 Sort Type Management
Our FHgraph class, coming soon, will have occasion to compare two FHvertex objects. At certain times (like when it's testing whether two vertices are actually the same vertex), it will want to use the data member as a basis for comparison. At other times (like when it's comparing two vertices' distances to a third reference vertex), it will want to use the dist member as a basis for comparison.
We'll use the machinery used throughout the quarter, and augmented last week, to manage a sort key for FHvertex:
static int sortKey;
static stack<int> keyStack;
static enum { SORT_BY_DATA, SORT_BY_DIST } sortType;
static bool setSortType( int whichType );
static void pushSortKey() { keyStack.push(sortKey); }
static void popSortKey() { sortKey = keyStack.top(); keyStack.pop(); };
The implementation of all these methods has been discussed, but you'll see everything again when we reveal the entire class, which we do now.
10A.4.6 The Full FHvertex Listing
We will use the following includes in our graph development:
#include <limits.h> #include <utility> #include <vector> #include <queue> #include <set> #include <map> #include <stack> #include <iostream> #include <functional> using namespace std;
Here, is the entire FHvertex class. We have now documented all the code you are about to see either in this, or in last week's lesson.
// CostType is some numeric type that expresses cost of edges
// Object is the non-graph data for a vertex
template <class Object, typename CostType>
class FHvertex
{
// internal typedefs to simplify syntax
typedef FHvertex<Object, CostType>* VertPtr;
typedef map<VertPtr, CostType> EdgePairList;
public:
static int sortKey;
static stack<int> keyStack;
static enum { SORT_BY_DATA, SORT_BY_DIST } sortType;
static bool setSortType( int whichType );
static void pushSortKey() { keyStack.push(sortKey); }
static void popSortKey() { sortKey = keyStack.top(); keyStack.pop(); };
static int const INFINITY = INT_MAX; // defined in limits.h
EdgePairList adjList;
Object data;
CostType dist;
VertPtr nextInPath; // used for client-specific info
FHvertex( const Object & x = Object() );
void addToAdjList(VertPtr neighbor, CostType cost);
bool operator<( const FHvertex<Object, CostType> & rhs) const;
const FHvertex<Object, CostType> & operator=
( const FHvertex<Object, CostType> & rhs);
void showAdjList();
};
// static const initializations for Vertex --------------
template <class Object, typename CostType>
int FHvertex<Object, CostType>::sortKey
= FHvertex<Object, CostType>::SORT_BY_DATA;
template <class Object, typename CostType>
stack<int> FHvertex<Object, CostType>::keyStack;
// ------------------------------------------------------
template <class Object, typename CostType>
bool FHvertex<Object, CostType>::setSortType( int whichType )
{
switch (whichType)
{
case SORT_BY_DATA:
case SORT_BY_DIST:
sortKey = whichType;
return true;
default:
return false;
}
}
template <class Object, typename CostType>
FHvertex<Object, CostType>::FHvertex(const Object & x)
: data(x), dist((CostType)INFINITY),
nextInPath(NULL)
{
// nothing to do
}
template <class Object, typename CostType>
void FHvertex<Object, CostType>::addToAdjList
(FHvertex<Object, CostType> *neighbor, CostType cost)
{
adjList[neighbor] = cost;
}
template <class Object, typename CostType>
bool FHvertex<Object, CostType>::operator<(
const FHvertex<Object, CostType> & rhs) const
{
switch (sortKey)
{
case SORT_BY_DIST:
return (dist < rhs.dist);
case SORT_BY_DATA:
return (data < rhs.data);
default:
return false;
}
}
template <class Object, typename CostType>
const FHvertex<Object, CostType> & FHvertex<Object, CostType>::operator=(
const FHvertex<Object, CostType> & rhs)
{
adjList = rhs.adjList;
data = rhs.data;
dist = rhs.dist;
nextInPath = rhs.nextInPath;
return *this;
}
template <class Object, typename CostType>
void FHvertex<Object, CostType>::showAdjList()
{
EdgePairList::iterator iter;
cout << "Adj List for " << data << ": ";
for (iter = adjList.begin(); iter != adjList.end(); ++iter)
cout << iter->first->data << "(" << iter->second << ") ";
cout << endl;
}
The only method that really needs a small comment is showAdjList(). It is directly above. While short, it demonstrates how to use the map iterator to move through the list. I would ask you to study this two-line loop and make sure your knowledge of STL maps and iterators is adequate to get you through the understanding and, if need be, emulation of this loop. It is very simple, yet very important. (We could have declared showAdjList() to be const, but it would have required a little support and adjustment to other methods/members. Since we are exposing the data publicly to our client class, FHgraph, I chose not to do it.)
I am going to break tradition and not give a sample client. You can do that on your own. The class obviously works or I would not have presented it, and we need to move ahead with the introduction of the next ingredient in our algorithms, a class that will allow our algorithms to define and manipulate edges outside the context of a particular graph. That will be our next template class FHedge.