Section 2 - Minimum Spanning Trees

10A.2.1 Three Minimum Spanning Trees Problems

I will now use the terms vertex and edge more freely since you have a good idea of their meaning as representatives of the specific objects in a problem (city, flight, router, optical fiber, etc.). Our next exploration involves the design, rather than the use, of a product. By that, I mean that we are trying to figure out how to build something, and our job as programmers, is to help the engineers, architects, city planners, etc. know exactly what needs to be built.

Sometimes we are dealing with a one-off problem: we are involved in a five year project to build a new computer infrastructure in the state of Nevada. Other times we might be designing an interactive software application that will be used by thousands of designer/clients (a VLSI layout design package or an architectural design package), and our algorithm will be incorporated into the design package without a specific end-user application in mind. Either way, the problem is the same: we are trying to solve a problem called the "Minimum Spanning Tree" (MST) or "Shortest Spanning Tree" (SST) problem.

10A.2.2 A Sewer System

I thought it would be nice to start off with something low-tech for a change. Low tech, yes, but about as critical as it gets - sewage distribution systems. We are designing one as part of a new city planning project in Lake Oswego, OR, and our goal is to connect all the building sites to the sewage treatment plant. Since this is a new master plan, we don't have too many constraints. But what is the best way to do this? This is a graph theory problem with the building sites making up the vertices and the sewage pipes being the edges.

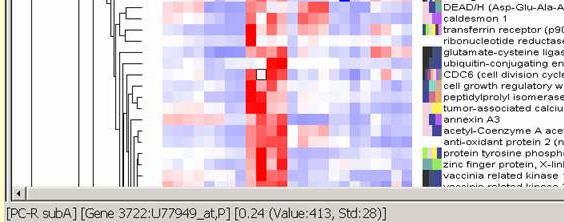
One way, called a star graph, is to connect each building site (vertex) directly to a master vertex (the treatment plant). This is called a star network. If we did that, it would look something like this (STP is the sewage treatment plant vertex):

An example of a city with 23 thousand sites served by one plant would have a total length of all edges (pipes) 102,998 miles.

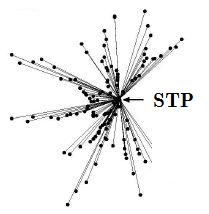
Obviously, every building site does not require a dedicated line to the STP vertex, and so we begin looking for a graph that connects everyone to the STP with a minimum total edge length. If we do so, we will get a minimum spanning tree (MST) that looks like this:

Total sewage pipe length? 421 miles. Since this represents not just the cost of the pipe, but also the grading and excavation to install the pipe, minimizing the total edge length is of major importance. Also note that we don't care what the length is between any one building site and the STP. So this is not a shortest path problem.

I picked a sewage problem here, but of course there are many such construction problems, both civic and architectural, that would fall into this exact form factor:

1. Gas Pipelines
2. Fiber Optic or Cat-6 network cable in a high-rise building
3. Street or highway design.

These problems all have non-directional graphs since we are counting exactly one edge between any two vertices.

10A.2.3 VLSI or Schematic Design

Next, consider an application software package that is used by chip or PC makers which allows layout designers to convert a logical electronic circuit (created by an EE) into an actual, physical layout that is used to manufacture the chip or PC board. Cadence, Synopsys, Magma and Mentor are examples of these products. In most cases, there are tens of thousands of transistors on a single chip, and they each need to be interconnected electronically. There are many different pathways, but we will focus our attention on just one aspect: the electrical power grid (i.e., the voltages and grounds designated by layout designers using terms like VDD or VSS). This grid will connect all the transistors together, and it needs to be done using minimum length, all other things being equal. (In practice there are many constraints - the chip layers and other pathways that must be avoided, but an MST algorithm still applies).

10A.2.4 The Human Genome Project and Gene Expression Patterns

There are many more examples of minimum spanning trees in industry, but I thought I would end the list with a somewhat advanced application called Gene Expression Patterns. Gene expression is the term used to describe how the genetic patterns (i.e., DNA configuration) in the individual cells of all living organisms (be they human, yeast or plant) relate to the actual functioning and structure of each cell. In other words, it is about how the mathematical coding of the gene expresses itself physically, biochemically, behaviorally, physiologically and through other characteristics unique to individual organisms and all their specialized cells.

The reason that gene expression has become such an active field in the last 10 years is due to the enormous amount of genetic data available due to research efforts like the Human Genome Project. Scientists have mapped the genes on human chromosomes, which means that they know exactly what they are and where they are. However, this is merely a mathematical pattern. Only a small fraction of these gene patterns are really understood. What do they do, and what happens when individuals have slight variations in the patterns?

The reason that this is such a hot topic for us, is that one of the main tools in understanding gene expression is mathematical clustering -- the recognition of individual patterns or groups from a large data set where the groups don't immediately present themselves. Exactly why clustering is used to understand gene expression is beyond the scope of this overview. However, medical researchers are generating large data sets from the genetic code and the physical testing of the cells, and from those data sets, they are looking for clusters or patterns.

In any given cell, some genes are switched "on" meaning that they are used as a template to manufacture proteins, and some are turned "off" or deactivated. Each cell has a different pattern of on and off genes, but it is not easy to predict, based on knowing this pattern, what that means to the cell. Does one pattern express itself as a tendency towards heart disease, obesity or a particular cancer?

Guess what one of the most important new tools in this study is? Minimum Spanning Trees. To show one example of this, I have excerpted a diagram of a computer program written at the Oak Ridge National Laboratory which uses an MST generator as part of its design.

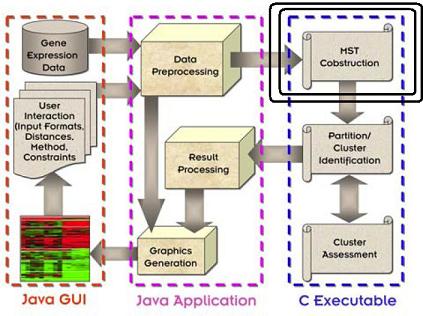
You may find it interesting that both Java and C (which is used for speed required to do the computation) were used to implement the program (called EXCAVATOR). I have circled the component that does the MST graph algorithm. It uses something called the kruskal method to compute the MST, and in the next few days you will fully understand kruskal's method and even have an actual C++ implementation of it.