Section 7 - The Seven Segment Display
SSD.7.1 The Seven Segment Display
Let's look at seven very special boolean functions which, together, are used thoughout computing to display numeric digits on LEDs: these are the seven elements of the seven segment display.

As you can see, there are actually 16 common patterns plus decimal point. However, we'll focus mostly on the first 10, digits 0 - 9.
A seven segment display consists of seven seperate units, or segments, which are usually named a, b, c, d, e, f and g. There is also a decimal point, but let's ignore that for this lecture.
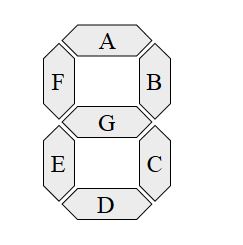
Can we express each of these seven segments in terms of boolean functions? Yes. First, they are either on or off (true or false), so the output is consistent with a boolean function. Second, the inputs are non-negative integers, again, consistent with boolean functions. What is the range of input ints? We only need 0 - 9, but even for that, four input bits are required, meaning that we can define the ouputs for inputs 10 - 15 however we wish.
There are two common choices. First, we might define the output for 10-15 all so that they display the letter "E" as in "Error". Or, we may choose to dispaly them as their hexadecimal equivalents: A, b, C, d, E, F. (Why do we use lower case for b and d?)
Let's look at the table that represents just one of these seven segments: the horizontal segment a along the top. When the input is 0, we want a to light up. So segA[0] = true. When the input is 1, we don't want a to light up. So segA[1] = false. Continuing in this manner we get the full truth table. I'm going with the alternative in which we express the letters A, b, C, d, E, F for inputs 10 - 16.
| input | a |
|---|---|
| 0 | T |
| 1 | F |
| 2 | T |
| 3 | T |
| 4 | >F |
| 5 | T |
| 6 | T |
| 7 | T |
| 8 | T |
| 9 | T |
| 10 | T |
| 11 | F |
| 12 | T |
| 13 | F |
| 14 | T |
| 15 | T |
I'll let you look up the tables for the remaining six segments.
That's all for this module. On to your lab.