Section 5 - Boolean Functions
BOOL.5.1 Boolean Functions
A subject of intense interest and research in computer science is that of boolean functions (or logic gates). These are functions that have one or more binary inputs (input bits) and one or more binary outputs (output bits). Such functions can be built using a special class of functions which only have one output bit. Here's an example with three inputs and one output:

Each of the inputs, A, B and C, can take one of two values: true or false (or if we prefer, 1 or 0). The output, Z, can be either true (1) or false (0).
How many possible inputs are there? Count them: ABC can be 000, 001, 010, ... , 111, in binary notation, or 0, 1, 2, ..., 7, in decimal integer notation. So this particular function can be thought of as taking an int from 0 to 7 as input and a boolean (true or false) as output.
These are the beasts we want to study today. It turns out that the most complicated and open problems in computer science can be reduced to, or described by, such boolean functions. One studies the circuits that implement these functions and asks questions about how fast the circuits grow as we increase the number of inputs.
BOOL.5.2 Some Important Unary and Binary Boolean Functions
We are all familiar with boolean operators OR (||), AND (&&) and NOT (!), operators of computer programming. Their output value (true or false) is determined by the boolean values of one input (in the case of the NOT operator) or two inputs (in the case of the OR and AND operators) . Here are the tables that define the OR and AND operator:
| a | b | a||b |
| true | true | true |
| false | true | true |
| true | false | true |
| false | false | false |
AND
| a | b | a&&b |
| true | true | true |
| false | true | false |
| true | false | false |
| false | false | false |
These operators are now seen to be boolean functions which have two boolean (or binary) inputs and one boolean (binary) output. Here are the same tables shown in binary form with the common mathematical symbols:
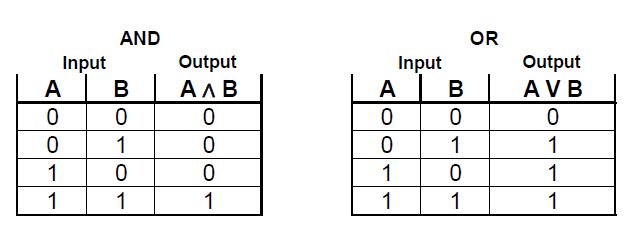
How many other boolean functions are there that have two inputs and one output? Same question for functions with one input and one output. (You can discuss this in the forums.)
Here is the important unary funciton NOT (unary means one input):
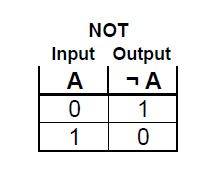
There are three more binary operations (or gates) which are commonly used in computer science and engineering, along with their symbols:


BOOL.5.3 Boolean Functions as Functions of Integers
If we consider the two binary inputs, a and b, as a single decimal integer number, then we can represent the tables in the following way:
| input | ouput |
| false false → 00 = 0(dec) | false |
| false true → 01 = 1(dec) | true |
| true false → 10 = 2(dec) | true |
| true true → 11 = 3(dec) | true |
| input | ouput |
| false false → 00 = 0(dec) | false |
| false true → 01 = 1(dec) | false |
| true false → 10 = 2(dec) | false |
| true true → 11 = 3(dec) | true |
As you can see, we have turned our original tables, which took two boolean inputs (a and b), into equivalent tables that take a single decimal int input (0 - 3). Here are the tables for AND and OR expressed as functions of decimal ints:
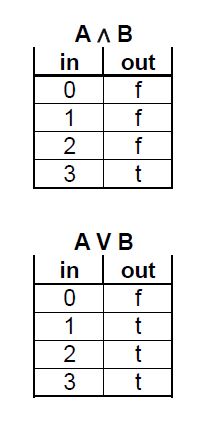
These two boolean functions -- and any other boolean function -- can be therefore represented in our programs as an array of bools (C++) or booleans (Java), the size of the array being the 2N, where N is the number of binary inputs. The input to the function is the index of the array, and the output is the boolean value stored at that position in the array. For the above gates with 2 binary inputs, the size of the table is 22 = 4, as you can see.
// C++ ---------------------------
bool orGate[4] = {false, true, true, true};
bool andGate[4] = {false, false, false, true};
// Java ---------------------------
boolean[] orGate = {false, true, true, true};
boolean[] andGate = {false, false, false, true};
Each array allows us to compute the answer to any input question by indexing the array:
// C++ ---------------------------
bool output;
// value of OR gate for input 2 (which corresponds to a true, b false:
output = orGate[2];
cout << "or[2] " << output << endl;
// value of AND gate for input 1 (which corresponds to a false, b true:
output = andGate[1];
cout << "and[1] " << output << endl;
// Java ---------------------------
boolean output;
// value of OR gate for input 2 (which corresponds to a true, b false:
output = orGate[2];
System.out.println("or[2] " + output);
// value of AND gate for input 1 (which corresponds to a false, b true:
output = andGate[1];
System.out.println("and[1] " + output);