Section 4 - Rational Numbers

5A.4.1 Rational Numbers

Rational numbers are defined to be the set of all numbers of the form:

num/den

where num and den are integers, and den != 0 (num is called the numerator and den is called the denominator).

A single rational number may have many forms, so we define the reduced form to be the one in which the numerator and denominator share no common factors and the denominator is positive. 

4/8, 300/600, (-20)/(-40) and 1/2

These are all the same rational number, with 1/2 being the reduced form.

In case a rational number has a reduced form with a 1 in the denominator we normally just write the numerator.

5A.4.2 An Example Using Rational Operators

Let's look at today's example. 

#include <iostream>
using namespace std;

// Rational prototype --------------------------------
class Rational
{
  // friend operators
  friend Rational operator+(Rational r1, Rational r2);
  friend Rational operator-(Rational r1, Rational r2);

private:
  long   num, den;
  long gcd();
  void reduce();
public:
  Rational(  long n = 0, long d = 1 );
  void show();
};

// main method ---------------------------------------
int main()
{
Rational q(-100,-25), r=3, s(-2,5), t(25,-100);
Rational ans;

ans = q + r;
q.show();   cout << "+";   r.show();
cout << " = "; ans.show(); cout << "\n";

ans = s - t;
s.show(); cout << "-";   t.show();
cout << " = "; ans.show(); cout << "\n";

ans.show(); cout << "+";   t.show();
cout << " = ";
ans = ans + t;
ans.show(); cout << "\n";

ans = s + 10;    // rational plus int???
s.show(); cout << "+ 10";
cout << " = "; ans.show(); cout << "\n";

return 0;
}

// Rational method definitions --------------------------
Rational::Rational(long n, long d)
{
// defaults in case of user error (bad d)
num = 0 ; den = 1;
if (d == 0)
return; // use defaults, above
num = n;
den = d;
reduce();
}

long Rational::gcd() // greatest common denominator of num and den
{
long temp, n, d;
for ( n = num,  d = den; d != 0;  )
{
temp = n % d;
n = d;
d = temp;
}
return n;
}

void Rational::reduce()
{
long gcDiv = gcd();
if (gcDiv)
{
num /= gcDiv;
den /= gcDiv;
}
if (den < 0)
{
den = -den;
num = -num;
}
}

void Rational::show()
{
cout << " " << num << "/" << den << " ";
}

// end Rational method definitions ---------------------

// overloaded operator functions   ---------------------
Rational operator+(  Rational r1, Rational r2)
{
Rational temp;

temp.num = r1.num * r2.den + r1.den * r2.num;
temp.den = r1.den * r2.den;
temp.reduce();
return temp;
}

Rational operator-(  Rational r1, Rational r2)
{
Rational temp;

temp.num = r1.num * r2.den - r1.den * r2.num;
temp.den = r1.den * r2.den;
temp.reduce();
return temp;
}

The output for this program is as follows:

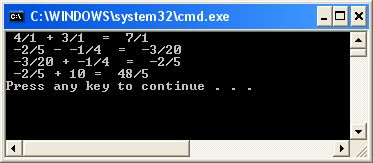
console shot

5A.4.3 Observations

There is a question in the source code. We add -2/5 to 10, an int.  But we didn't overload the + operator so that it took a Rational and an int.  So how did the program know how to get the correct answer?  Hint: re-read today's lecture if you don't know!

There are some improvements you could make to this example: