Section 6 - A Puzzle

2B.6.1 Mathematical Induction

Before ending this topic, I want to give you something entertaining to think about.  First, we return to the concept of recursion.

Recursion is a computational algorithm that is based on the more abstract concept of mathematical induction.  Mathematical induction is a technique for proving an assertion about all positive integers, n, which involves two steps.

If you can accomplish both steps, then the assertion must be valid for all positive integers n.

For example, let's prove that the alleged equality

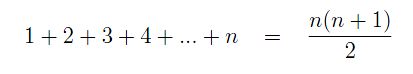
holds true for all positive integers n, no matter how large.

We prove that this holds when n = 1. 

By checking both sides of the assertion, we can see that they each evaluate to 1, therefore we have proved step 1.

Assume that the assertion holds for k and we will show that this implies it must hold for k+1. 

Start with the assumed truth for k, namely,

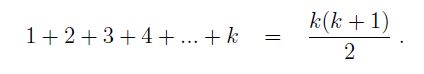
Now, we know that we can take any equation and add the same number to both side, and this will result in another true equation.  So we add k+1 to both sides of the last equality to get

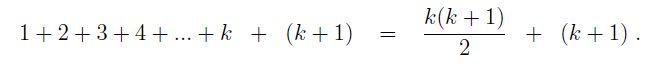
Re-arrange the right side using elementary algebra and we find

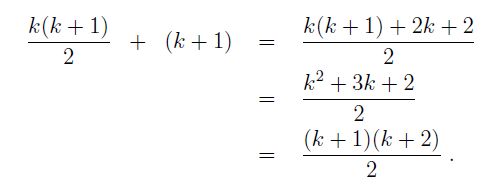
Together, the last two equations yield 

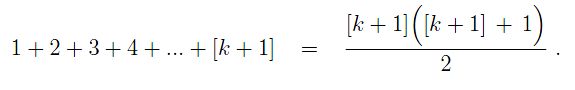
But look at this carefully: it is just our assertion when stated in terms of (k+1) rather than k. So this proves that the assertion is true for the integer k+1.

Since we have proved it to be true for k = 1, and we have also shown that if it is true for n = k, then it is also true for n = k+1, we have completed our proof in general. The equation must hold for all positive integers n.

Many mathematical truths that we know today are based on this kind of proof.

2B.5.2 A Famous Puzzle

The Isle of LOBUSUM  (LOgical BUt SUicidal Monks)

This is a famous puzzle which has an answer (i.e., proof) that anyone can find on the Web.  I encourage you to think about it on your own for at least a day or two before searching for the solution on-line.

There once was an island of 300 monks, some of whom had blue eyes, and those that didn't had brown eyes (and the monks knew this). They were also aware that there was no assurance that at any given time both or either color had to be expressed in the population: they could all be blue-eyed, all brown-eyed, or some of each, and this could change as the population changed due to births and deaths.

There were no reflective surfaces on the island, so no monk could see what he or she looked like, although they could each see all the others, and in fact did so on a daily basis.  Furthermore, these monks were highly intelligent, capable of solving any mathematical or logical puzzle instantly if there was enough information at their disposal.  Lastly, they had a strange cultural rule: if any one of them was to learn the color of his or her own eyes on any given day, that monk had to commit suicide at exactly midnight at the end of that day.  Needless to say, it was forbidden for the residents to speak about eye color, and no monk ever violated this rule.

For years, this population lived in peace and harmony with no suicides.  One day, a shipwrecked victim was washed ashore onto the island and the monks cared for the visitor for some weeks until she was healthy enough to return to the mainland.  A helicopter was summoned and the visitor made a short farewell speech.  She said. "I am forever indebted to you all for saving my life.  You have shown me great hospitality.  With your permission I will return in a year to see you all once more."  The group nodded, happily, in agreement.  As the visitor stepped into the chopper, she turned back at the smiling group and waved, adding, "I look forward to seeing some of your beautiful blue eyes upon my return."  As the helicopter flew off, the monks, pondering her words, became extremely distraught. 

When the visitor returned in a year, she found that all the monks had committed suicide.

Explain why, and prove (using mathematical induction) that there was no other possible outcome once the visitor had uttered her words.  Also, explain exactly when the suicides occurred, measured from the day that the visitor departed which you can call day 1.

For the purposes of explanation and class discussion, we will assume that, from the start, 100 of the monks had blue eyes and 200 had brown eyes, although there is nothing special about these numbers.  The same logic will apply to any breakdown of blue and brown eyes, except, of course, that at least one monk must have blue eyes, otherwise the visitor would not have mentioned blue eyes in her farewell speech.

There are no tricks or hidden variables.  This is a completely solvable (and provable) puzzle.  On-line, you will find many frustrated people who don't believe or understand the answer, but that's because those people simply do not comprehend mathematical induction.  You, on the other hand, are about to join the well-educated who can see the solution clearly.  We will discuss it over the next few days in the public forums.